滴下などのヘッド送液(head feed)での流量変化の問題を考えます。
自然流下という表現もします。
計算もしやすく流動や流体力学の練習としてよく出てきます。
ということは制御がしやすいということに繋がり、化学プラントなど安定的な運転が必要な場面では重宝されます。
バッチプラントで反応にヘッド送液が使われる理由が、この制御性にあります。
本記事を読むと、滴下の基礎的な内容を理解できます。
ヘッド速度(head feed)
ヘッド送液とは以下のような状況を指します。
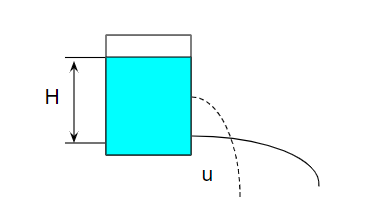
タンクに液が溜まっていて、胴から液体を排出します。
この場合の液の排出速度uは、ベルヌーイの法則にしたがいます。
$$ \frac{1}{2}ρu^2=ρgH $$
$$ u=\sqrt{2gH} $$
液体の高さHと重力加速度gだけで流速uが決まるという関係です。
ベルヌーイの法則はこの例では実際には抵抗係数を掛けたりして補正することもありますが、実務レベルでさっと計算するときには抵抗を無視したこの計算を良く使います。
例えばH=1.0mの時の流速u1は以下のようになります。
$$ u_1=\sqrt{2*9.8*1.0}=4.43m/s $$
液面が同じでも、液体を排出する胴高さを変えると、流速は変わります。
たとえはH=0.5mの位置から液を排出する時の流速u2は、以下のようになります。
$$ u_1=\sqrt{2*9.8*0.5}=3.13m/s $$
排出位置が高いほど流速が遅くなり、放物線にのっとって飛散距離は短くなります。
流量
実際の設備ではこの例のような大気に開放する例は少なく、配管で別の設備に移送します。
この時に大事なのが流量。
流量は単純に流速×口径で考えます。
例えば50Aの配管で、H=1.0mの時の流量を計算すると、断面積は0.00196m2なので
$$ 4.43*0.00196=0.00868 m^3/s $$
となります。
液量が変化する場合
タンクに液体が補充されない場合に液体が排出されると、流量は下がっていきます。
体感的にも理解しやすいでしょう。
計算式で考えると以下のようになります。
配管断面積をAとして、ヘッドHの時の流量Qは
$$ Q=A\sqrt{2gH} $$
となり、タンクの断面積をSとするとき、単位時間当たりのタンクヘッドの減少量は以下のように表現できます。
$$ -\frac{dH(t)}{dt}=\frac{Q(t)}{S}= \frac{A\sqrt{2gH(t)}}{S} $$
これを解くと、以下のようなイメージになります。
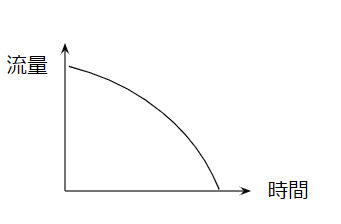
詳細の計算は不要
微分方程式を解くような計算は実務的には行いません。
- 最大排出速度を計算して、滴下完了予想時間を計算
- 排出流量を計算して、滴下に必要な流量制御の調整弁の計算。
こういう計算を行います。
バッチ運転の場合、各工程に余裕を設けます。
何か問題があった時に余裕がない工程設計をしていて、生産量が確保できないとなったら困るからです。
滴下の設計でも重要なのは、流量や時間に余裕があるかどうか。
詳細の計算モデルを立てて解いたところで、モデルの設計に漏れがあったり、計算時間が掛かったりと実務的ではありません。
簡単で直感的な計算式で、予測を立てるということの方が遥かに大事です。
参考
関連記事
最後に
流動の基本として、滴下などのヘッド送液の流速・流量の時間変化を解説しました。
単なるベルヌーイの法則だけの話で予測を立てて、運転に挑むことが現場レベルでは多いでしょう。
細かい計算をしようとすると、計算式が複雑になるのに精度はあまり出ないという問題が起こります。
これは化学工学的な計算のいろいろな場面で登場する問題でしょう。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。） *いただいたコメント全て拝見し、真剣に回答させていただきます。