粉体貯留ホッパーの形状の決め方について解説します。
ホッパーの設計は容積計算がメインになりますが、形状に関する選択肢はいろいろと持っておいた方が良いでしょう。
粉体の性質がずっと変わらない物だけを扱うなら、設置したホッパーを使い続ければいいですが、原料は往々にして物性が変わります。
特に、安息角はホッパーの設計と直結する要素。
意外なところで難しかったりします。
その難しさがわかれば、ホッパーの設計に対してかなり理解したと言えるでしょう。
安息角
安息角はホッパー設計上の粉体物性の重要な指標です。
粉体でも特にパウダー状であれば、粉の詰まり方・滑り方などの特性が1つの指標です。
粉体を平らな面の上に落として山の形を作ったとき、下の図のように円錐の角度は「安息角」と呼ばれます。
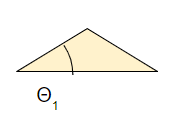
これが粉体の物性に依存します。
40°くらいが中程度の安息角であり、バッチ系化学プラントの粉体もこの辺りの値を取ることが多いです。
同芯ホッパー
ホッパーの容量を計算するとき、ホッパーの形状で場合分けができます。
まずは計算が簡単な同芯から。
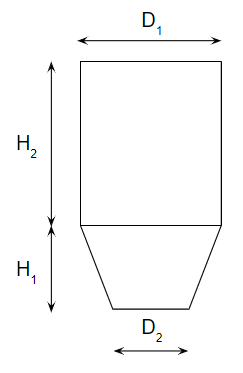
空間容積
空間容積は単純な算数の世界です。
コニカル部と直動部に分けて考えます。
コニカル部は
$$ V_1=\frac{1}{3}\frac{π}{4}({D_1}^2*(H_1+\frac{D_2}{D_1-D_2}H_1)-{D_2}^2*\frac{D_2}{D_1-D_2}H_1) $$
と表現できます。2つの円錐を引き算する形です。
これをちょっと整えると
$$ V_1=\frac{π}{12}({D_1}^2+D_1D_2+{D_2}^2)*H_1 $$
となります。
直動部は円柱の公式そのもので、
$$ V_2=\frac{π}{4}{D_1}^2H_2 $$
となります。
この合計値が、同芯ホッパーの空間容積となります。
粉体容積
ホッパー内に実際に粉体が貯留できる部分は、空間容積よりも少ないです。
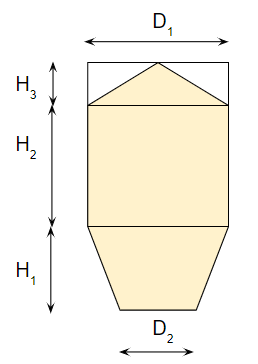
これは粉体に安息角があるからです。
とはいえ計算は単純です。
直動部の高さが低くなって、円錐として計算します。
$$ V_3=\frac{π}{12}{D_1}^2H_3 $$
安息角をΘ1とすると、
$$ \frac{D_1}{2}tanΘ_1=H_3 $$
という関係があります。
この計算では、ホッパー頂部のノズルがホッパーと同芯にあることを前提としています。安息角を考慮した円錐部の粉体体積はこれが限界です。入口ノズルがホッパーの中心からずれた場合に、安息角を考慮した粉体体積を求めることは難しいです。かつ、あまり意味がありません。
偏芯ホッパー
同芯の次は偏芯を見ていきましょう。
空間容量
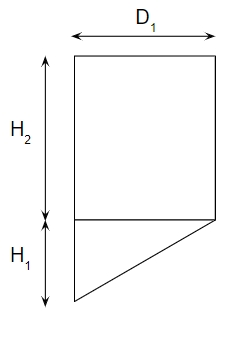
偏芯容量は計算自体は同芯と変わりありません。
ホッパー底の口径が小さくて無視可能な場合には、もっと単純な計算式になります。
偏芯のコニカル部の空間容量は、同芯のコニカル部の計算式でD2=0と置いて
$$ V_3=\frac{π}{12}{D_1}^2H_1 $$
と書けます。単純です。
粉体容量
粉体容量の計算は、ホッパー満杯まで充填する場合を考えると計算可能です。
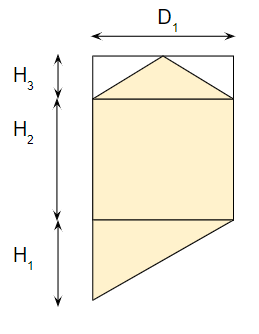
ホッパー頂部の入口ノズルがホッパーと同芯であることを前提と置いている点も、同じです。
コニカル部に中途半端に容量をためる場合の計算は、上部の円錐部の計算と同じで複雑であり、かつ意味がほとんどありません。
ホッパー容量の決め方
そもそもホッパーの容量はどうやって決めるものでしょうか?
これは貯留する粉体に依存します。
粉体重量
かさ密度
1バッチ当たりの処理量
重量やかさ密度は使用する粉体に固有です。
一方で処理量は調整可能です。
t跡えば、1バッチに2m3分の処理量があるプラントで、ホッパー空間容量が1.5m3くらいだとしましょう。
上の計算で粉体容量を計算したとして、1.1m3くらいしか溜めきれないとなったら、運転を2分割することを考えます。
バッチ処理であるがゆえに可能なことでしょう。
ホッパー容量は大きい方が好ましいですが、無理でも運転方法で対応できる部分が残っているということです。
参考
関連記事
粉体についてさらに知りたい方は、以下の記事をご覧ください。
最後に
粉体貯留ホッパーの容量計算の例を紹介しました。
空間容量と粉体容量は違いがあり、粉体の安息角が関係します。
同芯と偏芯で場合分けをしています。実務的には大きな違いはありません。
入口ノズルがホッパーの中心と同じかどうかで計算難易度が変わりますが、中心と同じとして計算しても実務上は大差ないでしょう。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。(コメント欄はこの記事の最下部です。)
*いただいたコメント全て拝見し、真剣に回答させていただきます。


コメント