タンク内の液を外部に放流する時の流量ってどれくらいですか？
こういう質問はたまにあります。
現場で放流作業をするときに、安全性をちょっと確認したい場合です。
簡単に計算できそうな気がして実はちょっと計算が必要なので、暗算では難しいです。
手計算レベルでチェックする方法を紹介しましょう。
いざ考える場面に直面したら、落ち着いて考えましょう。
対象モデル
今回は以下のようなタンクの下部にホースが付いている系を考えます。
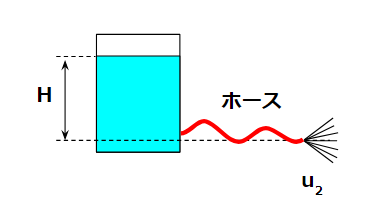
これは放流する液を特定の場所に集中させたい、通路上に放流させたくないなどの、経路調整のために使います。
以下のように、ホースを使わない場合とは少し違うという点に注意しましょう。
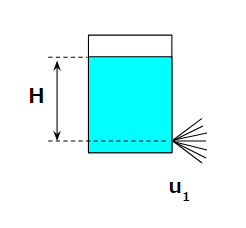
ホースがない場合
今回求めたいものは流量です。
流量を知るためには、先に流速を計算しないといけません。
流速の計算はエネルギー保存の関係から計算できます。
まずは、ホースがない場合を考えましょう。
タンク液面の位置エネルギーとタンク放出点での液の運動エネルギーが等しい、という関係を使います。
式としてはとても単純です。
$$ ρgH = \frac{1}{2}ρ{u_1}^2 $$
$$ u_1=\sqrt{2gH} $$
流量を求めたいのだから、口径×流速=流量の関係を使いましょう。
ここでいう口径は、放出点であるノズルのサイズです。
$$ Q_1 = \frac{π}{4}D^2u_1 $$
これで終わりです。
ホースがある場合
ホースがある場合は、この計算が少し変わります。
タンク液面は変わらないのですが、ホースを流れる部分で液体の圧力損失を考えないといけません。
$$ ρgH = \frac{1}{2}ρ{u_2}^2 + 4f\frac{1}{2}ρ{u_2}^2\frac{L}{D} $$
$$ u_2=\frac{\sqrt{2gH}}{\sqrt{1+4f\frac{L}{D}}} $$
項が1つ増えただけですが、それだけでとても面倒な気分になってきます。
だから現場レベルで計算しようとしても、ホースなしの場合で代用してしまいそうになります。
これが良いか悪いかは、ケースバイケースです。
具体的な数値例
具体的な数値で計算してみましょう。
H=1m、D=0.05mとします。
$$ u_1=\sqrt{2*9.8*1}=4.5 m/s$$
重力加速度9.8という数字も面倒なので10で考えて20の平方根は、4と5の間くらいで、42=16と52=25の真ん中くらいだから、約4.5という計算を私は頭の中で行います。
$$ Q_1 = \frac{π}{4}*0.05^2*4.5*1000*60=521L/min $$
こちらは口径50Aで平均流速1m/sなら100L/min程度なのでその4.5倍くらいで、450L/min程度とやはり計算を省略します。
ホースの場合は、計算が面倒ですね。
4f=0.04、L=10mとしておきましょう。
$$ 4f\frac{L}{D}=0.04*\frac{10}{0.05}=8 $$
ですので、
$$ u_2=\frac{4.5}{\sqrt{1+8}} =1.5m/s$$
$$ Q_2 = \frac{π}{4}*0.05^2*1.5*1000*60=174L/min $$
と極端に流速が低下して流量も低下することが分かります。
結果をまとめます。
ホースなし 4.5m/s 521L/min
ホースあり 1.5m/s 174L/min
ホースを付けただけで、結果が大きく変わりますね。
圧力損失の計算でホースの表面粗さを0.04と仮定を置いていますが、例えば0.01くらいの滑らかなものであっても流速2.6m/sとなり、ホースによる抵抗がやはり効いていることは理解できると思います。
損失の考え方
今回の例では、圧力損失を適正に判断することが大事です。
ホースという分かりやすい圧力損失を考えましたが、急いでいる場合にはこの項ですら計算を忘れたりします。
他にも計算に当たって考えるべきことを整理しておきます。
ノズルの急縮小
ホースなしの場合に圧力損失を考慮していない計算でしたが、ノズル部での急縮小は1つの項目になります。
ノズルサイズが変わっても流速は同じで、口径分だけ流量が変わるというのは簡易計算です。
ノズルサイズが小さい方が、ノズル手前での縮小による抵抗を受けるので、圧力損失として効いてきそうです。
私はここまで含めた計算をほとんどしたことがありません。
縮小部で損失は係数を含むから面倒ですよね。
急拡大の損失
吐き出し部は急拡大による圧力損失が起きます。
これも今回考慮していません。
縮小側は考慮しなくても拡大側は考慮した方が良いかもしれません。
急拡大の圧力損失は
$$ \frac{1}{2}ρu^2 $$
と考えるのが簡単でしょう。
これは、
$$ ρgH = \frac{1}{2}ρ{u}^2+\frac{1}{2}ρ{u}^2 $$
$$ u=\sqrt{gH} $$
としていることに等しいです。
ホースがない場合には他の圧力損失の項がないので急拡大部の抵抗が計算結果に影響を与えますが、ホースがある場合には影響は小さいです。
ホースなし 3.2m/s 370L/min
ホースあり 1.4m/s 162L/min
圧力損失の計算では、配管の摩擦損失などの主たる損失が明らかにある場合に行うので、急縮小や急拡大をわざわざ取り上げることはしません。
ただし、ホースなしの場合のように、他に何も考えることがない場合には注意しましょう。
バルブで絞る
ホースの前後にバルブが付いてあってそのバルブを絞って使う場合は、バルブの圧力損失は考えておきましょう。
厳密な計算ではCv計算をしますが、現場で手計算をするには向いていません。
こういう場合は、とりあえずバルブ面積×流速=流量として考えておけば良いでしょう。
これはホースなしの状態で、ノズル口径だけが変わるのと同じ考え方です。
例えば50Aのバルブ全開でホースなしで放流すれば、急拡大を考慮しても3.2m/sの流速となり、流量は370L/minです。
ここでバルブを絞って25A相当になった場合は、流速は3.2m/sのまま流量だけが下がって93L/minとなると考えます。
ホースがある場合にも、この計算結果に近くなると予想できます。
バルブの圧力損失 ＞＞ ホースの圧力損失、急拡大・急縮小の圧力損失
となるからです。
例えば、ホースの圧力損失は25Aとしてではなく50Aとして考えます。
50Aのバルブを25Aに絞った時、25A部の流速3.2m/sですが、50A部は1/4倍の0.8m/s程度となります。
圧力損失には口径の項が含まれますので、25Aに対する50Aの圧力損失としては1/8倍になります。
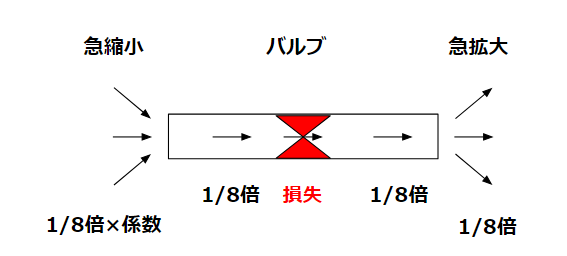
手計算レベルだとこれらの部分は含めなくても計算結果に大きな差は出ないでしょう。
もちろんホースの長さが長かったり、急拡大・急縮小の数が多かったりすれば、話は別です。
参考
関連記事
最後に
タンク内の液をホースを使って放流するときの流量計算の考え方を紹介しました。
エネルギー保存則と圧力損失の考え方がポイントです。
急拡大やホースやバルブなど、損失になりそうなものの何を考慮するかはケースによって変わってきます。
手計算でさっと確認したい場合に役経つ、現場向きの考え方です。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）
*いただいたコメント全て拝見し、真剣に回答させていただきます。
コメント