ポンプ圧力損失計算(pressure drop)は化学工学の教科書に載っていますが、計算がやや複雑です。
少なくとも手計算では不可能で、Excelや専用のソフトで計算することが多いでしょう。
とはいえ、現場レベルで即決する時には使えません。
そこで、現場でも使える暗算レベルまで、計算を簡略化してみました。
この内容が自由に使いこなせるようになると、製造課からの信頼感はいきなり急上昇するでしょう。
圧力損失計算の流れ
圧力損失計算の流れを紹介します。
化学プラントで機械設備などを設置したり能力検証をしたりする場合に、機械エンジニアが圧力損失計算をすることがあります。
圧力損失の計算は化学工学的に体系化されていて、教科書やネットにも多く資料があります。
私自身も記事にしていますが、実務上は簡易計算しか行っていません。
バッチ系化学プラントでの圧力損失を考える対象は、一般に以下の条件があります。
- 500kPa以下の液体
- 大気圧以下の気体
液体は密度が1000kg/m3、粘度が10cP程度であることが多いです。
フローをチェック
圧力損失計算をする前に、まずはフローをチェックします。
フローをチェックして「圧力損失を計算するかどうか」を判断します。
モデルとしては以下のとおりです。
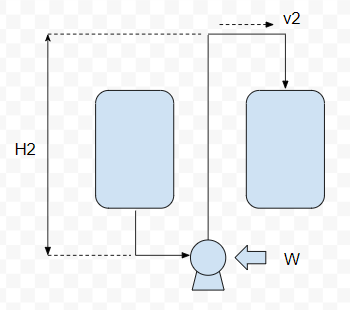
流速の把握
まずは流速を把握します。
場合によっては計算することもありますが、標準流速と標準口径を設計している会社が多いでしょう。
標準口径の考え方は液体を送る配管に限定されているのではないでしょうか？
気体だと温度圧力によって比体積が異なるため、流速で把握しにくいからですね。
流速を把握するかどうかは。以下のステップになるでしょう。
- 液体 標準流速と標準口径の関係から、配管口径をチェックする
- 常圧の気体 標準流速と標準口径の関係から、配管口径をチェックする
- 減圧下の気体 温度圧力を調べて比体積を計算して、流速を計算する
標準流速について詳しく知りたい方は、以下の記事をご覧ください。
流速を調べると言っても、まずは配管口径をチェックします。
ほとんどの配管口径は十分のはずです。
問題は1つの配管ラインで口径が上がったり下がったりする場合。
理由もわからずに配管口径を変えている場合は、標準流速の考え方ができていないケースが多いです。
バッチ系化学プラントでは、ガスラインの熱交換器出口で入口よりも配管口径が小さくなりますが、これが極端に配管口径が小さくなって、圧力損失が大きくなるというケースがあります。
こういう配管口径の変化がある部分は、要チェックです。
配管摩擦損失計算
さて、ようやく本題のバッチ系化学プラントの配管摩擦損失計算の実際を紹介しましょう。
実際は相当雑に行います。
だいたい以下のとおりです。
| ポンプ | 5～10m |
| ブロアー | 類似プラントから決定 |
| 真空ポンプ | 同じプラントの類似設備から決定 |
ほとんどこの思想でOKです。
ここで言いたいのは、「学術的な計算式を使う必要が無い」ということ。
初学者向けや精密計算をするときには、真面目な計算を行います。
その計算にだけ目を向けていれば良いわけではありません。
もっと重要なことが汎用性
運転管理者・保全担当者を経験すると嫌でも身に付きます。
真面目に計算した結果、予備品を共通化できないことがどれだけ現場を困らせるか。
ここに気が付いたら、設備設計の方法は変わります。
- 類似設備の情報を集める
- 設置予定の設備の運転条件・レイアウト・フローを眺める
- 設置予定の設備のスペックを決める
これでOKです。計算しません（笑）
プラント内の設備の思想統一という意味での計算はしますけどね ＾＾
配管高さ
配管高さはポンプ揚程に直結します。
どちらかというと、配管摩擦損失の方がマイナーの存在で、配管高さがメジャーなポンプ揚程の要素です。
下の図を見てください。プラントを横から見たイメージ図です。
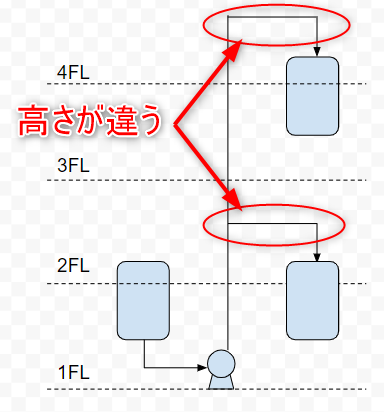
送液元のタンクの位置は変わらなくても、送液先のタンクの高さはいくつも候補があります。
2階に送る・3階に送る・4階に送る…。
この送り先タンクの高さに対して、配管高さはほぼ自動的に決まります。
私の働く工場では、1つの階が5mで決めているので、配管高さは以下のとおり簡単に決めることができます。
| 階 | 配管高さ(m) |
| 2 | 10 |
| 3 | 15 |
| 4 | 20 |
配管高さは「各階の天井までの高さ」という安全側で見ます。
5m高さの階で2階のタンクに配管を敷設する場合、最大でも7～8mになるでしょう。
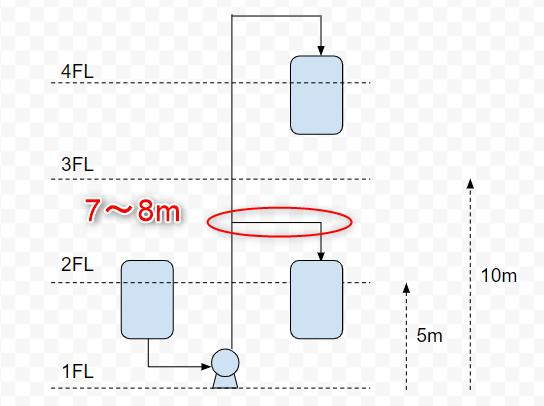
配管高さを10mでポンプ揚程計算に適用すると2～3mの余裕が、ポンプ側にできます。
配管抵抗
配管摩擦損失の計算上は、配管抵抗を計算しないといけません。
実際には、これは5～10mの世界です。
標準流速を1～2m/sに制限するからです。
5～10mといいますが、実際には5mか10mかの2択です。
下の図を見てください。プラントを上から見た図です。
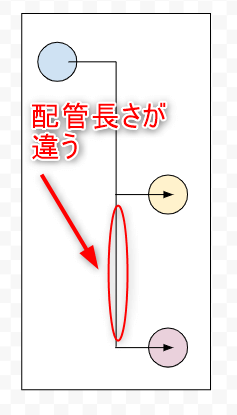
プラントは上から見ると普通は長方形の形をしています。
この中でポンプを中心に考えて、送液元と送液先の配管長さを考えてみましょう。
配管長さが短い時と長い時の2択があります。
| 配管長さ | 摩擦損失(m) |
| 短い | 5 |
| 長い | 10 |
これくらいのざっくりとした考えで十分です。
配管部品
配管部品は抵抗として真剣に考えないといけません。
下手に摩擦損失の数学的な計算をするよりもよっぽど大事です。
抵抗として考えないといけないものを、下に示します。
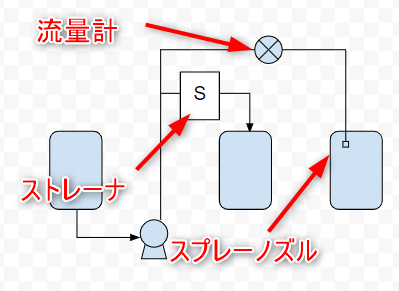
3大抵抗と私は勝手に呼んでいます。
これらは配管流れに対して「詰まりやすそうなもの」です。
ストレーナや流量計はとりあえず5mと見ることが多いです。
ちょっと真面目に考えるときもありますが、頻度は少ないです。
スプレーノズルはかなり真剣に考えないといけません。
スプレーノズルの仕様をメーカーに確認する必要があります。
ここを適当に5mとして考えてポンプを買い、
いざスプレーノズルの仕様が20mと分かったときは、手遅れ。
通常はポンプ設計 → 配管設計（スプレーノズル設計）としがちですが、これでは失敗します。
スプレーノズル設計 → ポンプ設計というように優先順位を変えないといけません。
他にも、「詰まりやすいもの」の仕様はポンプ設計より先に決めないといけません。
ポンプの圧力損失計算の公式
ポンプの圧力損失の計算は公式があります。
先に下の図を見てください。
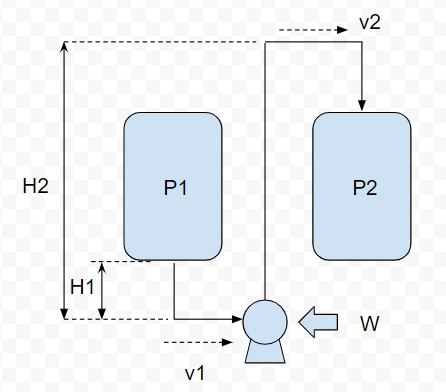
ポンプの圧力損失を計算するときの公式は、一般に以下のとおり書きます。
$$P_1+ρgH_1+\frac{1}{2}ρ{v_1}^2+W=P_2+ρgH_2+\frac{1}{2}ρ{v_2}^2+ΔP_2$$
これ、ちょっと複雑ですね。
言語化する方が楽かもしれません。
（送液元のエネルギー）＋（ポンプが流体に加えるエネルギー）＝（送液先のエネルギー）
これが基本的な関係です。
送液元のエネルギー、送液先のエネルギーというのは以下の3つから構成されています。
- 圧力エネルギー
- 位置エネルギー
- 速度エネルギー
ポンプが流体に加えるエネルギーはここでは、
$$W$$
として簡略化して表現します。
ここに、配管摩擦損失を考慮します。これを
$$ΔP$$
として簡略化して表現します。
配管摩擦損失の計算式
配管摩擦損失の計算式を示します。
$$ ΔP = 4F\frac{1}{2}ρv^2\frac{L}{D} $$
これは表記方法は教科書によって様々ですが、考え方は当然同じです。
配管摩擦損失は運動エネルギーに比例
圧力損失は運動エネルギーに比例します。
運動エネルギーは流体力学の場合は、
$$\frac{1}{2}ρv2$$
で定義されます。
圧力損失とは、摩擦損失そのものです。
摩擦損失は速度の2乗で定義するのが普通。
速度の絶対値で定義する分野もありますが…。
密度が高い方が、摩擦損失が高いことも体感的に理解できるでしょう。
水と空気ではどちらが圧力損失が大きいか。水ですよね。
それらをまとめて、圧力損失は運動エネルギーに比例すると考えます。
下の図で、同じ配管を流れる物体の、速度が速い下段の方が圧力損失が高いということになります。
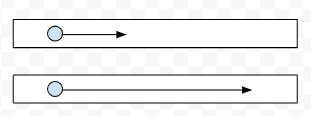
配管ルートに比例
圧力損失は配管ルートに比例します。
配管ルートといってもここでは簡易的な表現を使います。
$$\frac{L}{D}$$
Lが配管長さで、Dが配管直径です。
配管が長く・細いほど抵抗が大きいです。
配管長さLが長いほど、抵抗が大きく
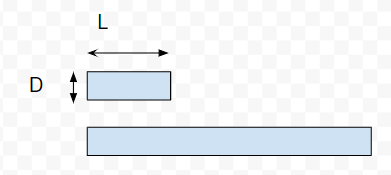
配管直径が細い方が、抵抗が大きいです。
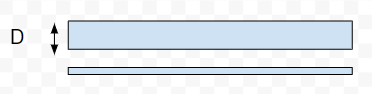
これも直感的に理解しやすいですよね。
配管形状という場合、エルボ・チーズ・レデューサなどのフィッティングを考えないといけません。
フィッティングに掛かる摩擦損失を、配管の長さ〇ｍ分の摩擦損失に置き換えます。
これを相当長さといいます。
配管が複雑であるほどLが大きいという意味ですね。
イメージ的には下の図を確認してください。
エルボなどの曲がりを、真っ直ぐな配管に置き換えるイメージです。
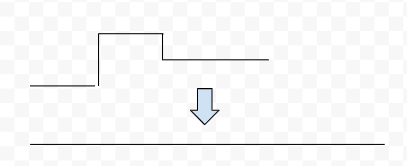
配管の粗さに比例
配管摩擦損失は配管の表面粗さに比例します。
目に見えにくい部分なので、意識しにくいですけどね。
土の地面と氷の地面をイメージすると分かりやすいでしょう。
配管内でも、鉄・ステンレス・フッ素樹脂ライニング配管で粗さは異なります。
配管摩擦損失の計算例
バッチ系化学プラントの配管摩擦損失の計算例を紹介します。
不要な項を削除
上記の公式を整理するところから始まります。
- \(P_1=P_2=0\)
- \(H_1=0\)
- \(\frac{1}{2}ρv^2=0\)
- \(ΔP_1=0\)
これを以下で整理して解説します。
\(P_1=P_2=0\)
バッチ系化学プラントでは送液前後のタンク内の圧力はゼロと考えます。
- タンクは全て大気に開放されている。
- バッチ運転では全量送液が基本。
- 工程の最初か最後に送液する。
この思想から、送液時の圧力はゼロとみなします。
\(H_1=0\)
送液元のタンクの高さはゼロと考えます。
厳密にはタンク底からポンプまでの高さを考えることは、ごくまれにあります。
その高さも考えずにゼロとする方が、安全側です。
実際には、タンク内の液高さは利用可能なエネルギーです。
これを期待して、「ポンプに必要な揚程を計算しない方がいい」という意味です。
\(\frac{1}{2}ρv^2=0\)
そもそも運動エネルギーが全体に占める割合は非常に低いです。
v = 1～2m/sで考えるのが普通です。v = 2としても、ρ=1000(水）の場合で、
$$\frac{1}{2}pv^2=\frac{1}{2}*1000*2^2=2$$
位置エネルギーとしてH=10mで考えた場合
$$ρgH=1000*9.8*10=98$$
となります。
圧倒的ですね！
無視して良いという量です。
\(ΔP_1=0\)
これは「v1 < v2」 という関係から出てきます。
送液元の配管口径 ＞ 送液先の配管口径であると
$$v_1<v_2$$
となります。
「送液元の配管口径 ＞ 送液先の配管口径」とするのは、ポンプ吸込み側でのキャビテーション防止のためです。
配管口径が1サイズ変わると、25%程度は口径が変わりますので
$$\frac{v_1}{v_2}=(\frac{1}{1.25})^2=0.64$$
圧力損失は流速の2乗で効いてくるので
$$(\frac{v_1}{v_2})^2=0.64^2=0.4$$
ΔP1（吸込み側）では圧力損失の計算で重要な運動エネルギーが、かなり小さいことが分かりますね。
これに配管長Lや配管口径Dを考えると、ΔP1はΔP2に比べて無視可能であることが分かります。
整理後の公式
上記の不要な項を削除した、整理後の公式を見てみましょう。
$$W=ρgH_2+ΔP_2$$
これだけです。
とても簡単ですね！
実際の計算で考えるモデルはここまで簡略化できます。
これは計算プロセスが非常に単純になることを意味します。
- 配管高さを決める
- 配管摩擦損失を計算する
- ポンプの揚程が決まる
この原則はバッチ系化学プラントのポンプ圧力損失計算で非常に重要です。
配管摩擦係数 4f
配管摩擦係数は4fだったりλだったり表記が微妙に違います。
moody線図を使う方法が一般的です。
バッチ系化学プラントでは
$$4f = 0.02$$
くらいで十分です。
というのも、液の密度・粘度がほぼ変わらず、配管口径設計を標準流速で考えるから。
これだけでレイノルズ数Reがほぼ一定になります。
配管も鉄やステンレスなど形状が決まっています。
配管の表面形状で決まるε/dの要因も固定化されています。
ここから4fという配管摩擦係数は0.01～0.03くらいの範囲で収まることが多いです。
配管摩擦損失計算の最も面倒な配管摩擦損失計算をざっくり仮定することは、
計算ステップを大きく簡素化できます。
流体の運動エネルギー
流体の運動エネルギーは以下の部分です。
$$\frac{1}{2}ρv^2$$
水でρ=1000、速度を1m/sで考えると
$$\frac{1}{2}ρv^2 = \frac{1}{2}×1000×1^2 = 500$$
ここも簡単ですが、詳細計算をしても桁が大きく変わるような結果にはならないのでOKです。
配管形状
流体の運動エネルギーは以下の部分です。
$$\frac{L}{D}$$
ここは影響が出そうなファクターですよね。
仮にL=50、D=0.05として進めましょう。
50mはバッチ系化学プラントのサイズとしてはかなり高めです。
0.05mm、つまり50Aもバッチ系化学プラントでは標準的。
$$\frac{L}{D} = \frac{50}{0.05} = 1,000$$
配管摩擦損失の結果
計算結果をまとめましょう。
$$ΔP =4f \frac{1}{2}ρv^2 \frac{L}{D} = 0.02×500×1,000 = 10,000 (J)$$
計算結果の単位がJなので、m単位に置き換えるために
$$ρg$$
で割り戻します。
水なのでρ=1000、重力加速度gは9.8くらいですが、ざっくり10。
$$ρg = 1000×10 = 10,000$$
ですので、
$$ΔP = 1 (m)$$
という結果になります。
配管高さや弁の損失を5m単位で考えるので、1mの配管摩擦損失は無視可能であることが良く分かりますね！
結果に対する簡単な検証
仮定で雑に扱っていた、配管摩擦損失4fも2倍に上がったところで、配管摩擦損失は2mになるだけ。
配管口径50Aが25Aにしても流速が変わらないのであれば、配管摩擦損失は2mになるだけ。
流速が変わると影響は大きいのですが、その分だけ流量を下げる方向で運転します。
結果として、配管摩擦損失は上がる要素があまりないことが分かります。
例外は存在しますが、配管摩擦損失の計算式とその結果を知っていると
応用として例外に対応することはできます。
配管ルートと圧力損失の簡易計算
バッチ系化学プラントでよく見る配管を例に圧力損失の簡易計算の結果を示します。
ポンプアップの場合
バッチ系化学プラントの圧力損失の計算で最も多い場面を最初に紹介します。
下の図のようなポンプアップの場合です。
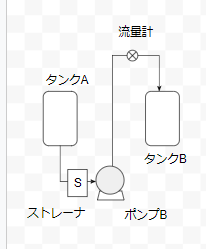
ここで圧力損失計算が必要な要素とその数値を紹介します。
| 項目 | 要素 | 損失(m) |
| タンクA内圧 | 運転条件 | 0 |
| ストレーナ圧損 | メッシュサイズ | 0 |
| ポンプB能力 | 揚程 | 揚程 |
| タンクB高さ | 配置 | 10～20 |
| 流量計圧損 | CV計算 | 5 |
| ポンプ吸込圧損 | 配管圧損 | 0 |
| ポンプ吐出圧損 | 配管圧損 | 5 |
| タンクB内圧 | 運転条件 | 0 |
吸込条件は無視
バッチ系化学プラントではタンクAからタンクBに液を送る時には、吸込み側はフリーになっています。
連続工場のように、タンクAの条件が制約条件になることはありません。
タンクAの圧力は0、ストレーナ圧損も0、ポンプ吸込圧損も0
この条件で考えることが普通です。
ストレーナの圧損は考えてもいいのですが、キリがありません。
タンクAの高さがある程度あれば、ヘッド圧でストレーナの圧損をカバーできることが普通です。
吐出条件は配管・高さ・CV
吐出条件で考えるべき要素は、配管の摩擦損失・配管高さ・CV、この3つです。
バッチ系ではタンクBもタンクAと同じでフリーになっていることが普通だからです。
タンクBが加圧状態でポンプを動かす場合もありますが、それは極めて限定的です。
配管の摩擦損失や高さは、ポンプの揚程計算で必ず考える項目ですね。
CV計算は、ライン中に調整弁があれば、という前提が付きます。
バッチ系でポンプアップしながら流量調整をするというのは、あまり多くはありません。
全くないというわけではありませんが、流量を制限するときにポンプを使わない方が多いです。
というのも、ポンプは圧力を上げることはできても、劣化等による変動が起こりえるからです。
流量を制限するというのは、運転上必要な流量を確保したいという制約があるから。
そこに不確定要素であるポンプを使うことは少ない。
というのがバッチ系の思想です。
その他、特殊な条件について以下のようなものがあります。
- ストレーナ 5m
- 出口ノズルがスプレータイプ 5～10m
ヘッドの場合
ポンプアップと対立する関係に、ヘッドがあります。
これは以下のような場面。
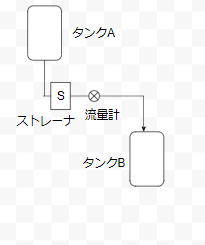
ポンプアップの場合と同じで、圧力損失計算に必要な要素をリストアップします。
| 項目 | 要素 | 損失(m) |
| タンクA内圧 | 運転条件 | 0 |
| ストレーナ圧損 | メッシュサイズ | 0 |
| タンクB高さ | 配置 | -5 |
| 流量計圧損 | CV計算 | 5 |
| 配管圧損 | 配管圧損 | 0 |
| タンクB内圧 | 運転条件 | 0 |
タンク高さと流量計圧損
ヘッドの場合も、ポンプ圧損と同じで、タンクA内圧・ストレーナ・タンクB圧損は0でいいでしょう。
これに加えて配管圧損も0
というのも、ヘッドの場合は流速は非常に小さいからです。
ポンプのように高い圧力が出るわけでなく、流速が遅いと配管摩擦損失はほぼ無視可能。
ということで、タンクA～タンクBの高さの差と、流量計のCVの値だけでほぼ決着が付きます。
タンクA~タンクBの高さを5mとして考えていますが、これは工場のサイズや配置によって変わります。
高さの差が1mも取れない場合は、要注意！
CV計算も満足のいく結果が得られないことがあります。
この場合は、以下のような対応をします。
- タンクAを加圧しながらヘッドで落とす（タンクA内圧を上げる）
- 常に一定量はタンクAに貯めるように運転方法を変える（タンクA~タンクB高さを取る）
性能曲線の基本的な解釈
ポンプの性能曲線とはポンプの能力を知るための重要な曲線です。
一般に以下の図のような形をしています。
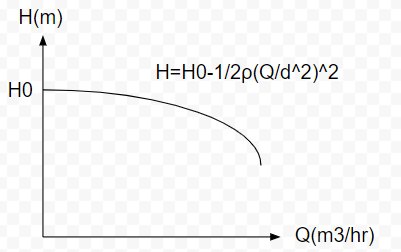
この図は、ある1つの曲線を書いていますが、これだけではほとんど意味がありません。
いくつかの線図を重ねることで、ポンプの各種能力を示す重要な線図となります。
性能曲線の基本的な曲線について、解説します。
ベルヌーイの法則
ベルヌーイの法則というの法則が、流体力学で登場します。
ベルヌーイの法則とは、力学におけるエネルギー保存則を流体に適用したものです。
力学のエネルギー保存則とは位置エネルギー＋運転エネルギー＝一定という関係性を示した法則です。
これを流体のエネルギー保存則として一般化したものが、ベルヌーイの法則。
位置エネルギー＋運動エネルギー＋圧力エネルギー＝一定
という圧力エネルギーが追加された法則とも言えます。
位置エネルギーは
$$ρgh$$
運動エネルギーは
$$\frac{1}{2}ρv^2$$
圧力エネルギーは
$$P$$
でそれぞれ定義します。
ベルヌーイの法則は圧力の単位・ヘッドの単位など単位換算をして紹介すrケースがあります。
私は圧力の単位で揃えた今回の方式が分かりやすいです。
力学の位置エネルギーや運動エネルギーの質量mを密度ρに置き換えただけで関連付けれますから。
性能曲線とベルヌーイの法則
性能曲線はベルヌーイの法則と関連します。
上に示した性能曲線を再掲載します。
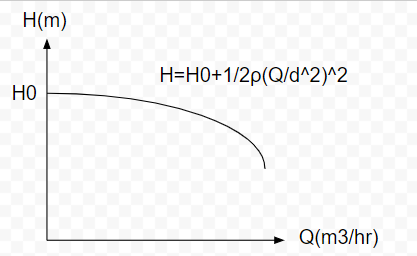
この曲線の意味を最初から解説しましょう。
横軸は流量
横軸は流量を示します。
m3/hやL/minなどポンプのサイズによってさまざまです。
縦軸は揚程
縦軸は揚程を示します。
これはポンプの性能が流量と揚程の関係で決まるからです。
縦軸は色々なパラメータを並べることで、いくつもの曲線を重ね合わせることができます。
性能曲線の解釈
ポンプの性能曲線は、
- 流量0で揚程はほぼ最大
- 流量が増えるにしたがって揚程が下がる
という関係にあります。
これが実はベルヌーイの法則と関連します。
ポンプが動く → 流体にエネルギーが加わる → 位置エネルギーと運動エネルギーに分散
という関係を示したものが、流量と揚程の関係です。
数式では以下のとおり書きます。
$$H=H_{0}+\frac{1}{2}ρ(Q/d)^2$$
HとH0はそれぞれ揚程です。
ρは密度、Qは流量、dは配管口径です。
Q/dは流速を示します。
流速をvとおくと
$$\frac{1}{2}ρ(Q/d)^2=\frac{1}{2}ρv^2$$
と表現できますよね。
なお、ベルヌーイの法則のうち圧力エネルギーが表現されないのは、
揚程の定義が「圧力＝0となる液面高さ」だからです。
圧損曲線と性能曲線の関係
唐突ですが、圧力損失は流量と圧力の関係で決まります。
詳細は以下の記事どおり。
圧力損失の計算式をもう一度記載しましょう。
$$ΔP=4f\frac{1}{2}ρv^2\frac{L}{D}$$
ここでポンプの圧力損失を議論するとき、以下の値が固定化されます。
$$f,ρ,L,D$$
fは配管の摩擦抵抗であり、配管材質や施工法が決まると自動的に決まります。
ポンプの設計をするときには、配管の仕様は決まっているので、fを変えるという思想は普通はありません。
Lは配管長さ、Dは配管口径であり、ポンプ設計段階で決まるものです。
LもDも設計要素の自由度は低いです。
送り先が決まるとLはほぼ決まります。
送液量が決まるとQもほぼ決まります。
内容物は自由度はありません。
これらの値が決まってしまうと
$$ΔP∝Q^2$$
という圧力損失が流量に比例（流量の2乗に比例）という関係が得られます。
圧力損失曲線と性能曲線の関係を見ていきましょう。
“圧力損失”曲線と性能曲線の交点が運転点
配管の仕様が確定してプロセスの仕様が決まると、ある1つの圧力損し曲線が得られます。
これに対して、ある1つのポンプの性能曲線を並べてみましょう。
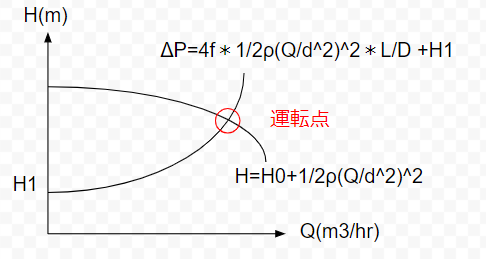
これは既定の配管に対して、新たなポンプを設計するときに、流量がどれくらい確保できるか。
というようなケースとしてよくある例です。
この2つの曲線の交点が運転点です。
配管の形が決まっているところに、流量を上げようとするほど必要なエネrぐぎーが高くなるのを示すのが配管圧損曲線。
1つのポンプで流量を上げるほど、揚液できる高さが変わる子を示すのが、ポンプ性能曲線。
配管とポンプの条件がマッチするところ
それが運転点です。めぐり逢いです。
ｎあお、H1は配管形状の最も高い位置にある点です。
配管圧損=配管高さ＋配管摩擦損失でほぼ決まります。
バルブを絞ると運転点が分かる
配管形状とポンプの能力から、ポンプの運転点が分かります。
でも、現場では「バルブを絞ると流量が落ちる」という現象を見かけます。
というより、家庭の水道でも同じですよね＾＾
これも性能曲線で議論可能です。
結論として、バルブを絞ると以下の図のようになります。
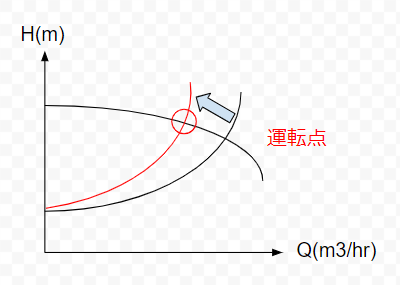
配管圧損曲線の角度が急になり、ポンプ性能曲線との交点が左にズレます。
左にズレるということは、流量が下がり揚程が上がるということ。
ホースの水を遠くに飛ばそうとするときに、先端を指で細くすると良いですよね。
あれも、バルブを絞るのと同じことが起こっています。
抵抗が増えて流量が少なくなっているけど、ポンプの能力は同じなので揚程が上がる。
こういう関係性があります。
バルブを絞るのは、毎管摩擦損失計算上は配管長さLを変える操作になります。
バルブ抵抗を直管相当長ととらえて議論しているためですね。
質量流量一定に騙されない
大学で流体力学を学んだ人の中には、質量流量一定の法則の罠にはまる人もいます。
$$ρAv=一定$$
Aが小さくなるとvが上がる。
絞りを入れても、質量流量は変わらないはずだ。
こう考えてしまいがち。
これはQが固定されているという前提があって初めて成立します。
送液能力が変わることを前提としていない学問的な話。
現実には供給能力や圧力損失の問題があります。注意ですよ！
動力曲線と性能曲線の関係
ポンプの動力周りのパラメータとしてモーター動力・軸動力・水動力の関係があります。
これらのパラメータは少し混乱するファクター。
整理しましょう。
モーター動力 → 軸動力 → 水動力 という流れがあります。
下の図を見てみましょう。
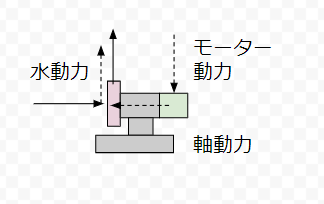
モーター動力はモーターに実際に入力される電力です。
軸動力はモーターの電力をモーターに変換して、機械的な力としてポンプ内の流体に加える力です。
水動力はこのうち、流体のエネルギーとして純粋に加わった力そのもの。
軸動力／モーター動力の値が高いほど、モーターでのエネルギー効率が良いという意味です。
水動力／軸動力の値が高いほど、ポンプの効率が高いtという意味です。
モーター動力・軸動力・水動力の大小関係を示すと、以下のとおりです。
水動力は物理的にきちんと定義されています。
水動力をPとおくと以下の関係があります。
$$ P=0.163ρQH $$
動力曲線と性能曲線の関係を見てみましょう。
動力曲線図
ポンプの動力曲線として、軸動力と効率の曲線を性能曲線に重ねるケースが多いです。
下の図のとおりです。
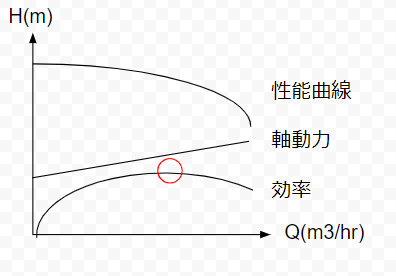
水動力はQの3乗
軸動力と効率の前に、水動力を見てみましょう。
水動力はQの3乗に比例する、Qに反比例するという関係があります。
$$ H∝Q^2$$
$$ P∝QH=Q^3$$
水動力が流量の3乗に比例するという関係は、モーターのインバータに関する話題としてよく出てくるお話ですね。
軸動力はQの1乗？
軸動力はQの1乗に比例しているように見えます。
実際には2乗や3乗に近いのですが、性能曲線と重ねると1乗に見えてしまいます。
ここでは簡易的に1乗とみなします。
ポンプ性能曲線においてQが変わってもHの変化量が極めて小さいからです
$$H∝Q^2 → const.$$
という関係とみなすと
$$P∝Q$$
という関係になります。
軸動力はQ=0、つまり締切運転でも一定の値を取ります。
これはポンプ内の流体を締切圧力まで上昇させるために、一定のエネルギーが必要だからです、
効率はQの2乗？
ポンプ効率は2字曲線で一定の流量でピークを持っているように目います。
効率はQの2乗くらいで効いているように見えます。
効率 = 水動力／軸動力という関係でありつつ、
水動力：Qの3乗、軸動力：Qの1乗であれば、
効率はQの2乗になるという計算です。
これが効率があるピークを持つという物理的な解釈です。
軸動力の欄でも記載しましたが、軸動力が完全にQの1乗でもなければ、3乗でもないので、正確な議論はできません。
ですが、傾向としては言えると思います。
効率についてはピークを持つ理由も解釈しましょう。
Q=0
Q=0、締切運転では、水動力=0で軸動力が一定の値です。
これは効率=水動力／軸動力=0という関係になります。
0<Q<max
Q=0から流量を上げていくと、ポンプ効率は徐々に上がっていきます。
低流量では、「水動力の増加量＞軸動力の増加量」の関係が出るので、
ポンプ効率は０からどんどん増加していきます。
高流量になると、「水動力の増加量＜軸動力の増加量」の関係が出てくるので、
ポンプ効率は徐々に下がっていきます。
この「水動力の増加量＜軸動力の増加量」の関係が変わる部分が効率ピークとなります。
Q=max
Qが最大の値になると、ポンプ効率は一定の値になります。
これは水動力も軸動力も一定の値を持つからです。
参考
関連記事
ポンプについて知りたい方は、先に以下の記事をご覧ください。
最後に
化学プラントの圧損計算について解説しました。
高さ・配管摩擦損失・圧力。
ベルヌーイの法則やポンプの圧損曲線・配管抵抗曲線の考え方を説明します。
実際には高さと詰まりやすい場所の圧損だけを考えるシンプルな計算でOKです。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）
*いただいたコメント全て拝見し、真剣に回答させていただきます。
コメント