圧力容器(pressure vessel)の強度計算を解説します。
細かな部分の計算まで含めるとかなり複雑になりますが、オーナーエンジニアでもここは知っておかないといけないという部分を、計算式を交えて解説します。
最近では潜水艦の圧壊でも話題になっている通り、圧力容器の設計は設備の安全上とても大事です。
バッチ系化学プラントでも、20号タンクや反応槽の設計をするときに、必ず使います。
基本的な部分をしっかり理解しておきましょう！
ジャケットなしの圧力容器(pressure vessel)強度計算
ジャケットなしの圧力容器の強度計算を見てみましょう。
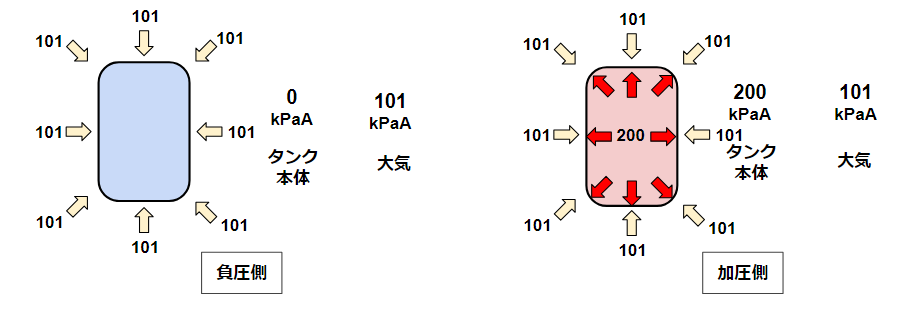
負圧/加圧という圧力方向のパターンと、胴部/鏡部という部位のパターンで、計4パターンあります。
負圧側
負圧側の強度計算式を見てみましょう。
加圧側の基礎式よりも複雑です。
胴部
胴部の負圧側の強度計算は多少複雑です。
- ①Lの計算
L=H+2/3h
- ②L/DとD/tの計算
- ③JIS B 8265の付属書からAとBの値を読み取る
- ④許容外圧を計算
最終的に使用する計算式は以下の通りです。
$$ P=\frac{4Bt}{3D} $$
式自体はとても単純ですよね。
計算プロセスが複雑になるのはBという係数が入っているから。
これをJIS B 8265の付属書のグラフから読み取るという作業が必要になります。
そのためには、Lという計算をしておかないといけません。
タンク形状が一般化されている化学プラントでは、グラフを近似式で置き換えれば、数値計算だけで計算可能となります。
鏡部
負圧側の鏡部の強度計算は以下の通りです。
- ①1.67倍の内圧を受けるとして計算
- ②球形胴の負圧の計算式の一部を読み替えて計算
- ③①と②の大きい方を採用
①の内圧を受ける場合の計算は、加圧側の鏡部の強度計算を見てください。
②の計算は、負圧側の鏡部と同じくAとBという付属書の読み上げが発生します。
かつ、使う計算式が若干変わります。
$$ P=\frac{Bt}{KD} $$
2:1半楕円の場合、K=0.9となります。
加圧側
加圧側の強度計算式を見てみましょう。
圧力容器の強度計算の基本的な部分です。
胴部
胴部の加圧側の強度計算式は以下の通りです。
$$ t=\frac{PD_i}{2ση-1.2P} $$
P≦0.385σηという条件は付きますが、低圧の圧力容器ならほぼこの式が適用できます。
圧力P、内径Di、許容引張応力σ、溶接継手効率ηで決まる式で、単純です。
分母の1.2Pの部分は計算結果である板厚を、1ランク上げるために考慮している部分と考えて良いです。
ηは小型低圧の一般的な圧力容器なら0.7とします。
放射性透過試験をすれば1.0となり必要な板厚を下げることができますが、検査をしないことが多いので代わりに板厚を上げましょうということですね。
鏡部
鏡部の加圧側の強度計算式は以下の通りです。
$$ t=\frac{PDK}{2ση-0.2P} $$
微妙に係数が違ったりしますが、基本的な形は胴側と同じです。
Kという係数が入っていますが、これは以下の値です。
$$ K=\frac{1}{6}(2+(D/2h)^2)=\frac{1}{6}(2+2^2)=1$$
Dはフランジ内径、2hは半楕円鏡板の内短径ですが、2:1半楕円鏡板が一般的ですので一定の値になります。
計算結果は、胴部の加圧側とほぼ変わりありません。
負圧と加圧の比較
強度計算では、以下の部分が分かりにくいです。
内圧に対して外圧にはどれくらい弱いのだろうか・・・
これを調べるには、計算式を若干整理すると良いでしょう。
胴部
負圧側の胴部の計算式
$$ t=\frac{PD}{4/3B} $$
BはSS400やSUS304などの一般的な物であれば、高くても50～100くらいの値です。
加圧側の胴部の計算式
$$ t=\frac{PD_i}{2ση} $$
1.2Pの部分は省略しています。
σはSS400やSUS304では100くらいの数字です。
計算式で異なる部分である、分母に着目しましょう。
| 分母 | η=0.7 | σ=100 | |
| 負圧① | 1.2ση | 0.84σ | 84 |
| 負圧② | 4/3B | 1.3B | 1.3B |
| 加圧 | 2ση | 1.4σ | 140 |
加圧側と負圧側①(1.67倍)の違いは、1.67という違いだけです。
1.67倍をするということは、分母に1/1.67(=0.6)という係数を掛けることと同じです。
ここでは分母に0.6を掛けて比較をしています。
負圧側①と負圧側②の比較は、84と1.3Bという値だけです。
Bが60～70くらいの範囲で、負圧側①と負圧側②の大小関係が入れ替わります。
加圧側と負圧側②の強度計算式を比較しても係数部分は、加圧側の2η=2*0.7=1.4で、負圧側は4/3=1.3とほぼ変わりません。
Bの値が100だとほぼ同じ値ですが、それより低いと必要板厚が増える側になります。
鏡部
負圧側の鏡部の計算式
$$ t=\frac{PD}{1/0.9B} $$
加圧側の鏡部の計算式
$$ t=\frac{PD}{2ση} $$
0.2Pは胴側と同じで省略しています。
胴側と同じように、係数の比較をしましょう。
| 分母 | η=0.7 | σ=100 | |
| 負圧① | 1.2ση | 0.84σ | 84 |
| 負圧② | 1.1B | 1.1B | 1.1B |
| 加圧 | 2ση | 1.4σ | 140 |
鏡の方が、負圧②の係数が低いことが分かります。
この分だけ、鏡部は必要な板厚が大きくなる方向です。
本体の板厚計算結果、胴よりもジャケットが1ランク板厚が高いことはよくあることですが、これは胴側1.3Bと鏡側1.1Bというところから推測が可能です。
Aの計算は、胴側と鏡側で異なるため単純比較はできないものの、オーダー比較という点ではこれくらいの簡易計算での推測は、体系理解に役立つと思います。
おまけ：ジャケットありの圧力容器(pressure vessel)強度計算
ジャケットありの強度計算も、ジャケットなしと同じように行います。
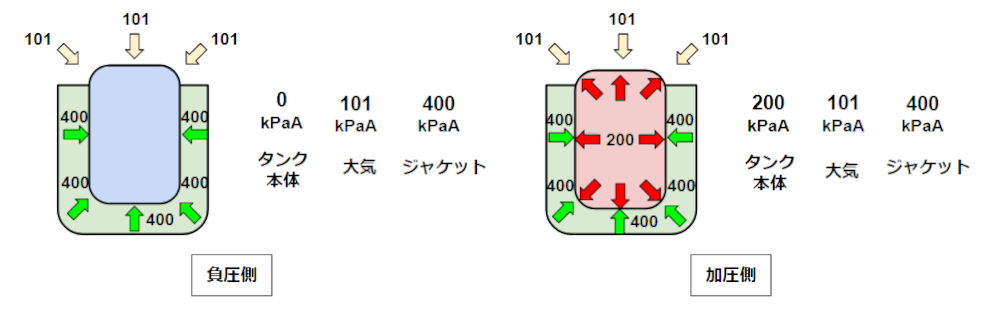
ジャケット有り無しでの違いは、ジャケットの加圧側の計算式でしょう。
というのも、本体側は2:1半楕円でジャケット側が10%皿型であることが多いからです。
10％皿型のジャケットの強度計算式は以下の通りとなります。
$$ t=\frac{PRM}{2ση-0.2P} $$
Rは10%皿型の場合、内径Dと同じです。
加圧側の2:1半楕円の強度計算式とほぼ同じ形であることが、分かります。
$$ M=\frac{1}{4}(3+\sqrt{R/r_0}=\frac{1}{4}(3+\sqrt{10})>2$$
Rとr0は皿型鏡板の円弧の半径を指しますが、10%皿型鏡板が一般的ですので一定の値になります。
M>2なので、計算結果である板厚は大きい側に出ます。
参考
関連記事
さらに知りたい方は、以下の記事をご覧ください。
最後に
圧力容器の強度計算の最重要部分を解説しました。
負圧/加圧と胴部/鏡部の計算式の比較です。
2:1半楕円と10%皿型という条件指定をして係数比較をしていけば、大小比較がしやすくなります。
付属書の係数Bは恐れるものではありませんね。
化学プラントの設計などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）
*いただいたコメント全て拝見し、真剣に回答させていただきます。