化学装置に断熱施工する場合、数量の見積として表面積計算(insulation surface)の実際を解説します。
断熱の数量は厚み×表面積で決まります。
工事の積算など金額に関する話になるので、表面積はしっかり計算しないといけない。
こんな風に考えるエンジニアが多いですが、意外と適当でも良いと思います。
伝熱計算の場合には、表面積の計算はしっかりしておいた方が良いでしょう。
なお、厚みは最適保温厚みの計算をすることで決まりますが、今回の記事では省略します。
熱交換器
断熱施工の対象となるのは、やはり熱交換器でしょう。
特に多管式熱交換器が多いです。
熱交換器に断熱を付ける場合、全面的に付けることが多いと思いますが、シンプルな計算のためにシェル側のみ断熱を付けるケースを考えます。
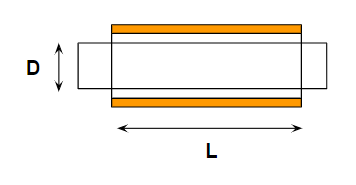
このケースは意外とありえます。
プロセス側が常温よりやや高くて、シェル側が冷水を通すという場合です。
常温より高いと気持ち悪いのでもう少し冷やしたいという場合です。
この断熱表面積の計算は以下の通りです。
$$ A = πDL $$
これだけです。簡単ですね。
タンク
タンクでも平型の円筒形を例に断熱量表面積の計算を行います。
このケースは、天板からの放熱を避ける狙いがあります。
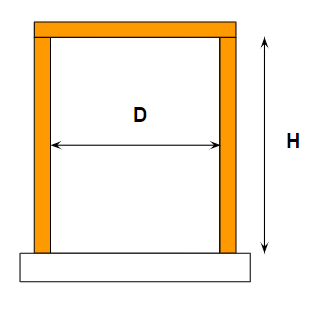
$$ A = πDH + \frac{π}{4}D^2 $$
これも簡単ですね。
Excelの簡単な計算式だけで処理できます。
皿型タンク
最後に皿型タンクの表面積計算を行います。
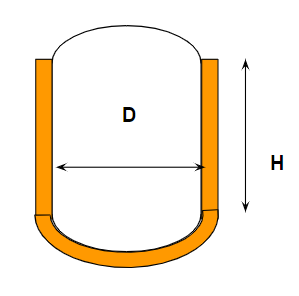
皿型タンクでも天板側は断熱を付けないケースは結構多いです。
さて、このケースで真面目に表面積を計算すると以下の通りです。
$$ A = πDH + 0.31514πD^2 $$
0.31514というのが面倒ですね。
上鏡も断熱を付ける場合は、2倍しましょう。
でも、この計算はほとんど意味がありません。
例えば、D=2m・H=3mという10m3程度のタンクを考えてみましょう。
計算結果です。
| πDH+0.25πD2 | 25.9m2 |
| πDH+0.31514πD2 | 27.8m2 |
断熱表面積は8%程度の違いです。
簡易計算として皿鏡を円板に置き換えてしまうと、8%くらい少ない数値で見積もることになります。
とはいえ、これは断熱工事全体のボリュームから見ると誤差範囲。
そのためだけに0.31514という数値を探してきたり、計算ソフトを使ったり・・・という面倒なことはしない方が健全でしょう。
鏡部分を完全に無視したらさすがに影響が出るので不安と思うなら、少し補正をしましょう。
以下のようなモデルを考えます。
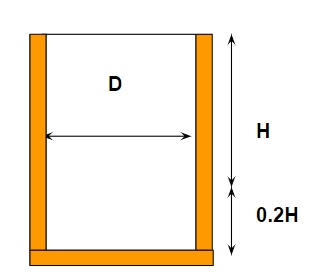
これは下鏡を完全に円筒に置き換えたものです。
H = 0.194Dですが面倒なのでH=0.2Dとしておきましょう。
この時の表面積は
$$ A = 1.2πDH + \frac{π}{4}D^2 $$
です。
比較してみましょう。
| πDH+0.25πD2 | 25.9m2 |
| πDH+0.31514πD2 | 27.8m2 |
| 1.2πDH+0.25πD2 | 29.7m2 |
今度は実際の計算より7%程度高いです。
ちょっと真面目にしようと思って鏡の高さの分を考えると、今度は高い目に出てしまいます。
とはいえ、どちらのケースでも±2m2くらいの差しかありません。
繰り返しますが、これくらいの差なら断熱工事全体の中では誤差範囲。
ユーザー側なら見積の積算速度を重視して、ざっくり計算しても良いと思います。
参考
最後に
断熱量の計算のための装置の表面積計算の例を紹介しました。
タンク・熱交換器を例にしますが、円と胴の計算だけでも十分に実用可能です。
皿鏡の表面積の計算は面倒なので、ざっくり丸めてしまっても良いでしょう。
伝熱計算の時にはこの簡易計算は使えませんので注意してください。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）
*いただいたコメント全て拝見し、真剣に回答させていただきます。