今回の記事では、皿型鏡板(head plate)の形状を解析します。化学プラントで非常によく使います。
加圧負圧など、大気圧以外の圧力で運転する設備が多いからですね。
こういう設備を設置する時は、消防申請など含めて公称容量をしっかり計算する必要があります。
実務上はメーカーのHPやカタログを見れば計算可能です。計算式が与えられています。例えば、北海のサイトを見ればそれて終わりです。
実は、容量の計算式は高校数学の範囲で解析することができます。
原理から深く理解したいという人は、一度計算にチャレンジしてみてはいかがでしょうか。
10%皿型鏡板(head plate)の形状
10%皿型鏡板の形状を確認しましょう。
モデルは下のとおり。
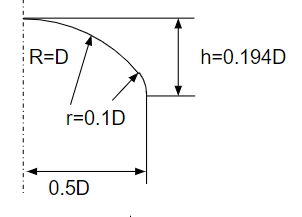
Rという大きな円とrという小さな円を重ね合わせた鏡形状をしています。
ここで、鏡直径Dに対して以下の関係性が提示されています。
- R=D
- r=0.1D
- h=0.194D
この関係を図面上で確認したり容量計算をしたりするのが、化学プラントの機械エンジニアの実務の1つです。
ところでこの\(h=0.194D\)ってどうやって導出されたかご存じですか?
答えられる人は意外と少ないはずです。
これが今回の記事のきっかけです。
Rとrの原点の関係
まずはRとrの関係を理解しておく必要があります。
数学的には以下の関係があります。
- Rとrは接点Aで接する
- 接点AでRの曲線とrの曲線は座標も傾きも同じ
- rの原点はRの原点と接点Aで結ぶ直線状にある

特に3番の「rの原点はRの原点と接点Aで結ぶ直線状にある」は意外に思うはずです。
これは鏡板のカタログなどには載っていません。
この関係が分かると、簡単にh=0.194Dが計算できてしまうから載せていないのでしょうか?
ちょっと不思議です。
鏡板(head plate)の高さ
鏡板の高さを実際に調べてみましょう。
先ほどの「rの原点はRの原点と接点Aで結ぶ直線状にある」が効いています。
下の図を見てください。
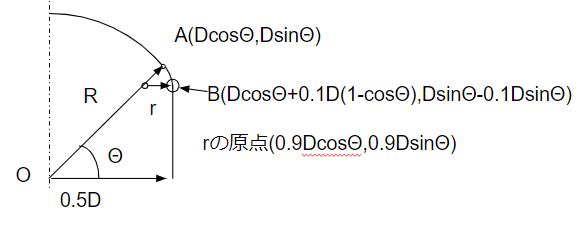
Rの原点Oを(0,0)としたx,y座標を考えます。
Rとrの接点Aの座標は\((D\cosΘ,D\sinΘ)\)です。これはΘの定義そのもの。
これを使うと、rと鏡直胴部の接点Bの座標は
$$(D\cosΘ+0.1D(1-\cosΘ),D\sinΘ-0.1D\sinΘ)$$
ちょっと分かりにくいですよね。
座標Aと座標Bの関係が、半径rの円で結ばれていることが分かれば、すぐに導出できます。
$$D(\cosΘ,\sinΘ)+0.1D(1-\cosΘ,\sinΘ)$$
と書く方が見やすいですね。
シンプルな関係です。
ここで「Bの座標は直胴部半径に等しい」という関係に着目すると、
$$D\cosΘ+0.1D(1-\cosΘ)=0.5D$$
という関係が得られるのでここから、
$$\cosΘ=\frac{4}{9},\sinΘ=\frac{\sqrt{65}}{9}$$
という関係が得られます。
R曲線のy切片と点Bのy座標の差
$$h=D-D\sinΘ+0.1D\sinΘ$$
に\(sinΘ\)の値を代入すると
$$h=0.194D$$
という関係が得られます。
鏡板(head plate)の容積
鏡板の容積の計算は、計算概念のみ示します。
容積計算は積分
$$\int_{y1}^{y2}\pi x^2dy+\int_{y2}^{y3}\pi x^2dy$$
から導出します。
項を2つに分けているのは当然ながら、R曲線とr曲線があるからです。
R曲線とr曲線はそれぞれ以下の関係があります。
$$x^2+y^2=R^2$$
$$(x-0.9D\cosΘ)^2+(y-0.9D\sinΘ)^2=r^2$$
ここからxについて式を変形して解けば、導出されます。
さすがにこの計算は学生時代までが限界ですね。
圧力容器設計の基礎図書
鏡に関する設計をする場合というのは圧力容器の設計にほぼ限定されるでしょう。
まずは圧力容器の設計の基礎から勉強しましょう。
この本が有用です。
座右の銘としたいですね。
関連記事
鏡板を使う設備として反応器やボイラーなどが該当します。
詳しく知りたい方は以下の記事をご覧ください。
最後に
10%皿型鏡板の形状解析紹介しました。
R=D,r=0.1Dからh=0.194Dという鏡高さを導出する方法を紹介しています。
鏡の容積を計算する数式の紹介もしています。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。(コメント欄はこの記事の最下部です。)
*いただいたコメント全て拝見し、真剣に回答させていただきます。


コメント