化学プラントで役立つ伝熱計算の基本｜3つの伝熱形態を実務的に理解する

　化学プラントの設計や運転において、「熱の伝わり方」を理解しているかどうかは大きな差になります。伝熱計算は、機械系の出身者にはなじみが薄いかもしれませんが、実務では避けて通れない分野です。
　この記事では、伝導・対流・ふく射の3つの伝熱形態を実務視点で整理し、化学プラントでどのように役立つのかを解説します。基礎を押さえるだけで、熱交換器や反応器の設計・解析がぐっと身近になります。

　伝熱計算は近似式や無次元数と使うことが多いので戸惑うかもしれませんが、概念といくつかの数字を知っていれば実務で十分に使えるでしょう。

この記事は、熱計算シリーズの一部です。
熱交換器の伝面計算だけを変えるときの考え方
熱交換器の伝熱面積だけを変えるときの計算方法
熱交換器の「汚れ係数」とは？設計で押さえたい基本と考え方
撹拌槽の伝熱計算の基本的な考え方
撹拌槽ジャケット下鏡の伝熱計算の考え方
伝熱計算の例｜化学プラント槽型反応器
プレート式熱交換器の熱容量計算とは？Q=mcΔTの基本と設計ポイントを解説
エアコンの冷却能力設計で大事な伝熱計算のイメージ

具体的な計算はこちらのフォームをご利用ください。

伝熱の3形態

伝熱つまり熱の伝わり方は伝導伝熱・対流伝熱・ふく射伝熱の3つのパターンがあります。

伝導伝熱

伝導伝熱は「熱が物質中を次々と伝わる」現象です。ポイントは動いている物がないこと。伝導なので動かずに伝えるという点が重要なのでしょう。固体物理学の分野で扱います。

伝導伝熱は物質中の伝熱をターゲットにしています。実質は固体に限定されていると思ってください。

以下のイメージ図を見てください。

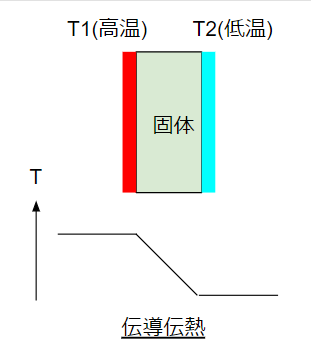
固体を挟んで片側が高温・反対側が低温だとします。この時に熱は固体中を伝わります。まぁ当然ですよね。

夏や冬の部屋で窓から熱が伝わるのはこのイメージです。空気は熱を伝えにく、魔法瓶はこの原理を使っています。伝導伝熱の計算では、フーリエの法則が適用されます。これは伝熱係数・厚み・温度差で決まります。伝熱係数が高いほど、厚みが小さいほど、温度差が大きいほど、熱が伝わりやすいという式です。非常に単純な関係式です。

厚み

厚みが小さいほど、熱は伝わりやすいです。家でも、壁が厚かったり、カーテンが厚かったりすれば、当然熱が伝わりにくいですね。もちろん、音も伝わりにくいです。音も熱も、固体内を伝搬するという意味で同じです。

化学プラントの設備ではこの厚みは変化させることが難しいです。厚みを増やすという事は、コストアップにつながります。厚みを減らすという事は、耐圧力が低くなります。ということで厚みを増やすことも減らすこともできないのが、通常です。

温度差

温度差とは、AからBに熱が伝わる時の、AとBの温度差です。温度差が大きい方が、熱が伝わりやすいです。感覚的に分かりますね。

この温度差を化学プロセス設計において変化させることは、通常は難しいです。プロセス側の要求は、運転条件・反応条件で決まります。

これに対して、温度調整をする手段が限定されています。スチーム・水・冷水・ブラインなどでしょう。使える冷媒は決まっていて、温度もほぼ固定されています。

厳密な温度調整をする場合は、特殊な冷媒を使いますが、そういうケースはあまりありません。ほとんどすべての伝熱計算では、温度差は固定されていると考えた方が良いです。

伝熱係数

伝熱係数は、熱が伝わりやすい物質の方が値が高いという物です。
・鉄・銅・アルミなどの金属が高いです。カーボンも熱が伝わりやすいです。
・逆に熱が伝わりにくいものとしては、ガラス、樹脂などがあります。

感覚的に理解しやすいと思います。2種類に分かれるということさえ理解していれば、細かい情報はネットや本で調べればいいだけです。化学プラントで使う材質は色々ありますが、その元をたどれば上記のような数種類に絞り込まれます。大学で勉強するまでもなく、ある程度の理科の興味があれば、日常生活で実感できる物ばかりです。その知識さえあれば、業務に簡単に応用できます。ところが、大学の教科書的な知識や、会社に入った後の勉強では、日常生活との結びつきをせずに、難しい話に入ってしまい付いていけなくなる人が多いです。

伝熱係数に関して言えば、無味乾燥な表があるだけです。解説も無く、表を見て自分で解釈しないといけません。

対流伝熱

対流伝熱は流体の温度差によって流体が移動して、温度が伝わる現象です。対流伝熱は伝導伝熱と違い、動きをイメージするものです。伝導伝熱のように、物の動きがない場所での伝熱ではありません。例えば以下のようなイメージです。

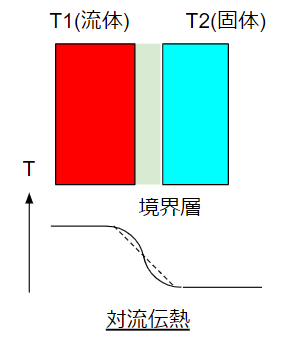
T₂という温度の固体は動きません。
T₁という温度の流体側は動きます。

流体と固体に温度差があり流体が動くことで、伝熱が進みます。もちろん流体が止まっていても熱は伝わります。これは伝導伝熱。流体が動くと熱の伝わりが速くなります。お風呂を温めるときにかき混ぜる方が速く均一な温度になりますよね。これと同じです。

流体の伝導伝熱以外に、流体そのものを動かして熱を伝えるので対流伝熱です。対流伝熱は物質をしていしたら決まるというものではありません。要素は複雑です。

対流伝熱の無次元数

対流伝熱の近似式は、非常に複雑ですが、次の関係式をまずは抑えておかないといけません。
　Nu∝Nu(Pr,Re)　強制対流
　Nu∝Nu(Pr,Gr)　自然対流
Nuはヌッセルト数、Prはプランドル数、Reはレイノルズ数、Grはグラスホフ数です。

Nu

Nuは対流熱伝達率と伝導熱伝導率の比を示しています。対流伝熱が起こる場合、対流源である流体と、別の物質との間の議論がなされます。この対流源は別の物質と違うものなので、必ず「境界」があります。この境界部とそれ以外とでは、色々な要素が違うために分けて考えます。

境界部を境界層といいます。対流伝熱はこの境界層の伝熱と考えても大きなズレはありません。対流源以外に、色々な要素の影響を受けます。境界部より外側の領域では、流体源そのものの特性だけで決まります。そこで境界層とそれ以外との比を取って、一般化しましょうというのがNuと私は解釈しています。

Pr

Prは動粘度と温度拡散率の比です。これも分かりにくいですね。動粘度？温度拡散率？なぜこういう要素が影響するのでしょうか？

温度の伝わり方そのものの解釈を考えないといけません。温度拡散率は、比熱・熱伝導率が大きな要素です。比熱とは熱容量そのものなので、「物質がどれだけ熱を保有できるか」ということと「その物質が周囲にどれだけの熱を伝えられるか」という比で決まる数字です。

温度拡散率はまだ分かりやすいですが、粘度はどういう意味でしょうか？熱の伝わり方に粘度が大きく影響するからです。

熱は、物質の分子が微小な動きを隣の分子に伝えることで、伝わっていきます。粘度が高いと分子の動きが遅いという事なので、分子間に伝わる熱の移動量も小さくなります。温度が高い方が粘度が低く温度も伝わりやすいので、温度拡散率に温度依存性を持たせる無次元数、という言い方もできるでしょう。

強制対流∝プランドル数Pr・レイノルズ数Re

強制対流は、ポンプ等の強制的な力で流体が動くケースです。強制的に動かす場合、レイノルズ数が大きな影響を与えます。レイノルズ数が大きいほど乱流、小さいほど層流です。乱流であるほど、速度が高いという言い方もできます。速度が高いほど熱は伝わりやすいですね。

自然対流∝プランドル数Pr・グラスホフ数Gr

自然対流ではレイノルズ数よりもグラスホフ数の影響を受けます。簡単に言うと浮力です。化学プラントの場合、自然対流に頼る装置が少ないため、あまり使う機会がありません。こういう概念があるという理解をしているだけで十分でしょう。必要な時に調べられたらそれでOKだと思います。

ふく射伝熱

ふく射伝熱は間に媒体がなくても伝わる熱です。伝導伝熱は固体が媒体になり、対流伝熱は流体が媒体になります。これらのモノがあることで熱が伝わります。

ふく射伝熱は違います。ふく射伝熱は、媒体がなくても伝わります。
　典型例は太陽光
太陽光を浴びると暑く感じますよね。これは太陽から放射される日航から熱を受けているからです。太陽光って宇宙から伝わりますよね。宇宙には固体はおろか流体らしきものもありません。モノ、つまり媒体がなくても熱が伝わるのがふく射伝熱です。イメージとしては以下の理解で良いでしょう。

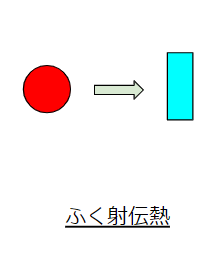
赤い熱を持ったモノから媒体がなくても、青い板に熱が伝わるイメージです。

伝熱形態と伝熱量

3種類の伝熱量の具体的な比較を行います。3種類の伝熱とは、伝導伝熱・対流伝熱・ふく射伝熱のことです。ふく射伝熱はバッチ系化学プラントではほぼ使いません。でも、ボイラーになると話は異なります。そこで、具体的な計算結果をもとに考えてみようと思います。

伝導伝熱

伝導伝熱の評価を行います。評価を揃えるために、単位面積当たりの伝熱量で議論します。

$$\frac{Q_1}{F_1}=λ\frac{T_{12}-T_{11}}{δ_1}$$

λ=40W/(m・K)、δ=0.1m(10mm)で考えましょう。ΔTを適当に振ってみます。

ΔT(K)	単位面積当たり伝導伝熱(W/m2)
10	4,000
100	40,000
1000	400,000

バッチ系化学プラントではΔTが10～100℃の世界なので、4,000～40,000W/m²くらいです。板厚は4～30mm程度で、特に多いのが10mmくらいなので、範囲としては大きなズレはないでしょう。

対流伝熱

伝導伝熱と同じで対流伝熱も、単位面積当たりの伝熱量で議論します。

$$\frac{Q_2}{F_2}=a_2(T_{22}-T_{21})$$

\(a_2\)は種類によって変わるので、パラメータとして振ってみます。逆にΔTは50℃で固定しましょう。ΔTはバッチ系化学プラントでは10～100℃くらいの範囲です。

\(a_2\)	単位面積当たり伝導伝熱(W/m2)	具体例
50	2,500	空気やガス
1,000	50,000	蒸気
5,000	250,000	水
50,000	2,500,000	蒸発・凝縮あり

水もしくは相変化ありの蒸発・凝縮がほとんどでしょうから、250,000～2,500,000という膨大な値となります。学生時代は対流伝熱は伝導伝熱よりも非効率的だと勝手に思っていましたが、そんなことはありませんね。

ΔT=10℃でも伝導伝熱よりも優れている計算です。

ふく射伝熱

最後にふく射伝熱です。

$$\frac{Q_3}{F_3}=εC_b{T_3}^4$$

\(ε\)は1で固定(理想的な黒体)として、\(C_b\)は5.67×10^-8 W/(m²・K⁴)野ステファン・ボルツマン定数を簡易的に1×10^-7で計算します。

\(T_3\)	単位面積当たり伝導伝熱(W/m2)
10	10-3
100	10
1,000	105

いかがでしょうか。ΔTが100℃くらいのバッチ系化学プラントでは全く話になりませんが、ボイラーなど1000℃の世界では対流伝熱に匹敵する伝熱量です。伝熱効率を上げるためには材料を何とかしたいが、強度的に必要な肉厚は決まっている。そうなると、ボイラーの伝熱効率は改良の選択肢が少ないことが分かりますね。

太陽熱はざっくり6000Kで考えると、10⁸(W/m²)のオーダーです。すごいですね・・・。

熱通過率と表面温度の関係

伝熱の学習をすると熱通過率の式に必ず出会います。

$$\frac{1}{K}=\frac{1}{a_1}+\frac{δ_1}{λ_1}+\frac{1}{a_2}$$

計算式自体は非常に単純で、熱伝導と熱伝達の足し算です。以下の式をまとめるだけですね。

$$Q=a_1(t_{11}-t_{12})F$$

$$Q=a_2(t_{21}-t_{22})F$$

$$Q=λ_1\frac{t_{12}-t_{21}}{δ_1}F$$

$$Q=K(t_{11}-t_{22})F$$

まとめた式を暗記したり、計算式に数値を当てはめているだけで、試験は合格します。実務で総括伝熱係数を計算するときもこれでOKです。

でも、物理的な解釈をもう1手間加えるだけで、理解はぐっと深まります。一歩進んだエンジニアを目指す人には、参考になる考え方だと思います。
　同じ熱量を伝えるにも、熱伝導率・熱伝達率が高いほど、温度差が低い。
これが熱貫流や総括伝熱係数を考えるときに効いてきます。

ここから物体の表面温度をイメージすることができるからです。

実務ではこういうアプローチで熱計算を行うだけで、表面温度を意識することは少ないのが実際でしょう。表面温度を考えるというのは、この意味では「重要ではないけど大事なこと」のカテゴリーに入ると思います。絶対に必要、というわけでは無い考え方ですからね・・・。

以下では、物体の表面温度を3ケースに分けて考えます。配管内外で熱を伝えるという一般的なシチュエーションを想定しています。

管内・管外ともに液体の場合

管内に液体・管外に液体という液液熱交を想定しています。この場合の、管周りの温度は以下のようなイメージになります。

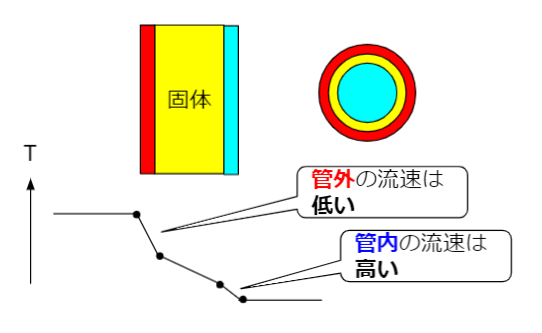
管外に温水・管内に冷水を通して、冷水を温めるというケースですね。赤色の部分が温水の熱伝達部分、黄色が配管の熱伝導部分、水色が冷水の熱伝達部分です。

ここで強調したいことは、赤色と青色の温度勾配。管外側の勾配の方が厳しく、管内の方が緩いです。言い換えると配管の表面温度は冷水側に近い温度になるということです。温水側の熱伝達率が低いので、温度勾配が付いてしまいます。温度勾配を付けないと熱が伝わらない、という方が正しいですね＾＾

さて、管外側の方の熱伝達率が低いのはなぜでしょうか？これは流速が小さいから。管の本数や、管外のバッフルの間隔で若干は左右される部分はありますが、普通は管外の方が流速が低くなります。管外の方が流路面積が大きいのが一般的ですからね。管の内と外で径が違うから面積が違うという理解からリンクさせても良いです。

「普通はこうなるはずだ」という予測をしながら、詳細計算を行って妥当性を検証するというプロセスを経る方が、単に計算式に数値を当てはめて終わりという考え方より1歩上の設計です。そのための拠り所の1つとして持っておきたい視点です。

管内が液体・管外が気体の場合

管内が液体・管外が気体の場合を考えます。

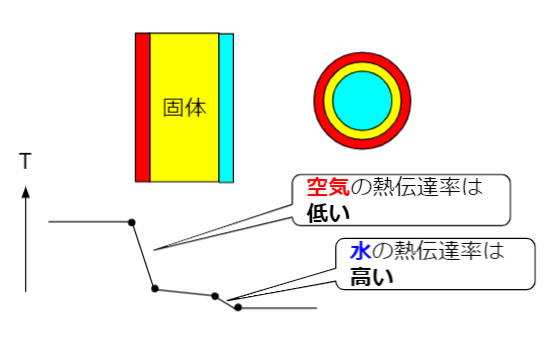
これは配管内の液体（水）が夏に温められるケースを想定しています。冬だと温度グラフを上下逆に考えればOKです。

ここのポイントは、空気と水の熱伝達率差。当然ですが、空気の方が熱伝達率が低いです。密度が低いから当然です。「熱伝達率が低い方が、温度差が高い」ですよね。

この結果、表面温度は水側に引きずられます。夏場に空の配管に手を当てると火傷しそうになりますが、水が入っているとそうではありません。配管内の水があることで表面温度が下がります。片側から加熱されて他方が冷却されていないことで熱くなるという意味で、夏場に車のボンネットに手を置いたり、車の中に入ろうとしたときにも同じような経験をできるでしょう。

管内で液体が蒸発・管外で蒸気が凝縮する場合

最後に、管内で液体が蒸発、管外で蒸気が凝縮するケースを見てみましょう。

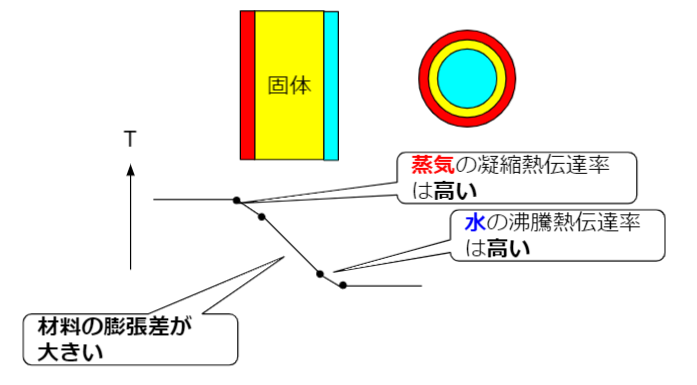
蒸気でプロセス液を蒸留させるというケースを考えています。蒸発・凝縮などの相変化を伴う熱伝達は急激に上がります。伝導伝熱と対流伝熱の差がかなり無くなります。

そうすると、伝導伝熱部分である固体の表面温度差が付くことになります。同じ物体の両側で温度差が付くと、膨張差が付きます。

最悪は亀裂や破損の原因となります。バッチ系化学プラントではグラスライニングやフッ素樹脂ライニングの破損を気にするときに、表面温度の話題がでます。

ボイラー特に水管ボイラーでは、管内が水・管外が空気の状態で、管内が沸騰という相変化を伴うため、管外面の温度は高くなく、水の沸騰温度の20～30℃程度と言われています。ボイラーの火室内は700℃をゆうに越えます。高圧水の沸騰温度＋30℃程度の300℃前後まで表面温度が下がると考えると、イメージが付くと思います。

風が吹くと対流伝熱が促進

風が吹くと対流伝熱が促進されます。これを伝熱工学の視点からちょっと見てみましょう。下の図を見てください。

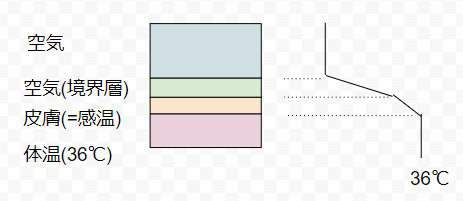
これは空気と人間の体温の間での温度勾配を、簡易的に書いたものです。外側の空気はいわゆる気温のことです。内側の体温は人間の体温。気温と人間の体温の間に、温度勾配ができます。

この2か所で温度勾配が起きます。風が吹いた時の影響を見てみましょう。

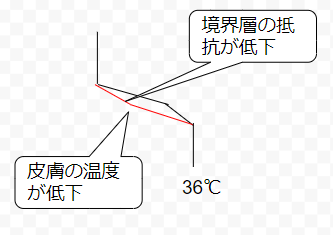
風が吹くと赤い線のように温度勾配は変わります。論理的には、下記の説明になります。

天気予報で気温の話を聞いても、実際に感じる温度が違うと思うことは多いでしょう。人間が実際に感じる気温を体感気温と言います。ここに風速の話が入ってきます。体感気温と風速の関係を以下に解説します。

0℃以上は風速は無視可能

日本でも中央より北の地域でなければ、0℃を下回ることは多くはありません。実際に、私も冬に風が吹いて寒いと思っていても、意識したことはあまりありません。
　風が拭いたら寒いな～
って感覚的に、瞬間的に感じていた程度です。もっと言うと「危機感」を感じるレベルではありません。

特に、温暖化の影響でどんどん温かくなってきているので、冬場でも防寒着を着なくても現場で動き回ることも可能になってきました。もちろん、防寒着を着る方が健康を維持できるので、付けた方が良いですよ ^ ^その気になれば、「防寒着なしでも耐えられる」という程度の話です。

0℃以下は体感気温 = 気温 – 風速

0℃以下になると、風速は体感気温に直結します。
　体感気温 = 気温 – 風速
この関係を嫌でも意識することになります。

‐5°℃の気温で風速5m/sなら、体感気温は -5 -5 = -10℃という計算をすれば、ほぼOK。とはいえ、気温-10℃・風速0m/sの体感気温-10℃に比べると、気温-5℃・風速5m/sの体感気温-10℃の方が、はるかに寒く感じます。

同じ体感気温でも感じ方は違う

体感気温が同じ-10℃でも感じ方は違います。
・気温-10℃・風速0m/sの体感気温-10℃であれば、目や耳が痛くなるということはありません。
・気温-5℃・風速5m/sの体感気温-10℃であれば、目や耳が痛くなり、歩くときに支障が出るレベルです。

風が吹いた瞬間に、歩くのをあきらめたり部屋に戻ったりしたくなります。外に出たことを後悔します。‐30°℃でも無風だと、しばらくは耐えることができますよ ^ ^

熱貫流量の単位

私が苦手としている内容です。熱貫流量という表現自体が私はなじみがありません。熱貫流量は熱量を時間で割った単位。単位時間あたりに流れる熱量なんて表現もできます。特に冷凍機やプレート式熱交換器などの熱交換をターゲットにしている設備の設計で登場します。

昔はkcalの単位を使用していました。私が入社する前も大学ではSI単位を使っていましたが、上司がkcal単位を使用していたので自然と使うようになってしまいました。今ではkWで表現することが多いでしょう。ところが、このkWとkcalって非常に間違えやすいです。

重要な指標な割に間違えやすいことなので、冷静に理解しておきたい内容です。

1kcal=4.2kJ

大前提として理解しておきたい単位変換式です。しにかろりーなどというごろ覚えもあります。これだけを理解していれば誤解は発生しないのですが、

厄介なのは1kJ=0.24kcalという関係があること。
1/4.2=0.24というのが本当にややこしい。
1kcal=0.24kJとか1kJ=4.2kcalなどの誤解が容易に発生します。kWという単位の方が最新で、kcalという単位が古いしんでいる単位なので、kcalはしんでいる単位だから、

という強引な結びつけをしています。それでも不安になるので、毎回変換を調べています。calはしんでいる。他に良い覚え方があれば教えてください。

kWとkcal/h

kWとkcal/hの単位変換は以下のとおりです。

これを覚える必要はほとんどありません。もっと重要なことは

このオーダーの感覚を肌感覚で理解することです。念のため、単位変換計算の詳細を示します。
　1 kW=1 kJ/s=1/4.2 kcal/s = 1/4.2*3600 kcal/h = 860 kcal/h
4.2と3600という数字が約1000倍差があることに着目するだけで、混乱を防ぐことができます。

10倍や100倍という中途半端な数字ではなく、1h=3600sという1000倍のオーダーで効いていることが理解のしやすさを手助けするでしょう。

冷凍機の例

例えば冷凍機などでは200,000kcal/hというようなkcal/h単位で表現することが多いです。これをkWに変換するには1000で割ればとりあえずOK
　200,000 kcal/h = 200kW
kWの方が桁が小さくてすっきりするという意味でも、kcalの方が古臭い感じがします。

このkWの単位で冷凍機を議論すると良いメリットは成績係数とリンクできるから。成績係数が4で200kWの冷凍機のモーター動力は約50kWと単純に計算できます。成績係数が4で200,000kca/lの冷凍機のモーター動力は？って聞かれると瞬間的に計算する人はほとんどいないでしょう。

kcal/hは体感的

kWで計算になれた人には分かりにくいかも知れませんが、kcal/hの単位には大きなメリットがあります。

それが熱計算を体感的に理解しやすいということ。水が10m3/hで流れていて温度差5℃で熱交換をする場合の、熱量は？というと
　50,000kcal/hと簡単に計算できます。
計算式だけ書くと、
　1000×10×5=50,000
となります。この発想はプラントの反応装置全体の冷却系統を検討するときに使います。いちいち50,000kcal/hを50kWに変換しても良いですが、結構面倒。

密度×流量×温度差というプラント設備で実際に測定できる生の単位系を使って、個々の冷却システムの熱量を計算して、それを合算する。その後に、合算後の結果がkcal/hでいったん算出した後に、kWに換算する。こういう扱いが好まれるでしょう。

総括伝熱係数Uも100kcal/(m2・h・k)などのkcal系で整理されているから、kcal系で理解する方が便利です。kW系に変換するためには、この辺の便利な単位系を全部変換しなおしていかないといけません。かなり大変な作業です。

参考

関連記事

さらに知りたい方は、以下の記事をご覧ください。

最後に

伝熱計算は、式を覚えるよりも「どの因子が支配的か」を理解することが実務では重要です。

• 固体を通す伝導
• 流体の動きを利用する対流
• 媒体を介さないふく射

この3つの伝熱形態の特徴をつかみ、総括伝熱係数の考え方を身につければ、熱交換器設計や反応器の温度管理にも応用できます。
複雑に見える伝熱の世界も、原理を理解すればシンプルに整理できます。

化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）
*いただいたコメント全て拝見し、真剣に回答させていただきます。

ブロトピ：今日のブログ更新