熱交換器(heat exchanger)の熱設計を、熱量の公式Q=mcΔtに基づいて解説します。
この公式は、熱の基礎知識として義務教育でも学ぶ内容です。
今さらと思うかも知れませんが、化学プラントでの熱設計はコストに直結する問題でとても大事です。
プラントの競争力を左右する重要な要素です。
現場の設計でどういう使い方をしているか、実際の設計例を紹介しましょう。
熱量Q=mcΔtが熱交換器(heat exchanger)設計の基本
熱量の公式Q=mcΔtの解説をしましょう。
熱量=質量×比熱×温度差
という関係があります。
これは比熱の定義がkJ/(kg・k)であることが先に来ています。
学校では、比熱の定義がそんなものだという風に与えられたことでしょう。
実務上もそれで大丈夫です。
一応、次元という意味でも整理しておきましょう。
| 熱量 | Q | kJ |
| 質量 | m | kg |
| 比熱 | c | kJ/(kg・k) |
| 温度差 | Δt | k |
熱力学を学んだことがあれば、時間で割ったものを日常的に使うことに気が付くでしょう。
| 熱量流量 | Q | kJ/s |
| 質量流量 | m | kg/s |
| 比熱 | c | kJ/(kg・k) |
| 温度差 | Δt | k |
化学プラントではこの熱量流量・質量流量を使いますが、流量をわざわざつけて呼ぶのは面倒です。
熱量の公式とほぼ同じ感覚で使ってしまっています。
比熱c
比熱cは決まった値（物性値）であって、設計者が意図的に変えることはしません。
材料によって比熱cの値はさまざまですが、工場で主要なものに限って整理しましょう。
| 水 | 1.0 |
| 鉄 | 0.1 |
| 有機溶媒 | 0.4～0.6 |
これくらいを押さえておけば、とりあえずはOKです。
有機溶媒は正確には個々の比熱を調べることになるでしょう。
プレート式熱交換器(heat exchanger)の計算例
熱量の公式を使う例を紹介します。
まずは簡単なプレート式熱交換器から。
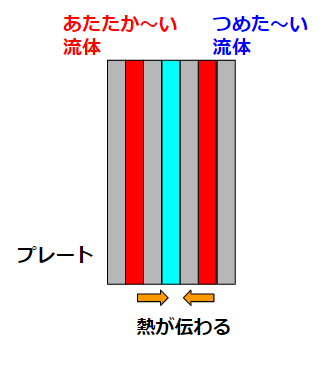
プレート式熱交換器では、温度の異なる2つの流体が流れることで熱交換をします。
温度の高い方を1、低い方を2と区分を分けて（添え字を付けて）、熱量の公式に関する情報を整理しましょう。
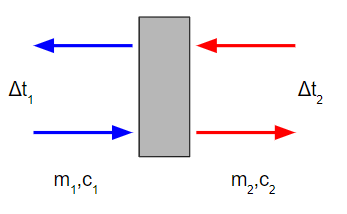
| 熱量流量 | Q1 | Q2 |
| 質量流量 | m1 | m2 |
| 比熱 | c1 | c2 |
| 温度差 | Δt1 | Δt2 |
例えば30℃の水を100L/minで流して60℃に温めたいという場合を考えます。
ここで、熱媒は90℃の温水を使います。
温水の流量をいくらにするか？ということが設計ポイントです。
流量を決めて、配管口径を決めていかないといけませんからね。
熱量Q1の計算
熱量Q1を先に計算しましょう。
Q1=100L/min*1kcal/kg/K*(60-30)K*1kg/L=3,000kcal/min
これは簡単ですね。
流量m2の計算
次に流量m2を決めたいのですが、温度差Δt2が決まっていません。
Q1=Q2は当然のこととして使います。
熱量を交換するのだから、感覚的には理解しやすいと思います。
ここは温度差Δt2を仮定してしまいます。
Δt2=10としましょう。
こうすると計算は簡単ですね。
m2=3,000/1/10=300L/min
温度差をいくらに設定するかということは実は難しい問題です。温水や循環水のように系外に排気しないのであれば、5～10℃くらいに抑えるのが無難です。というのも、温水なら冷えた温水を温めるためのスチームの負荷が・循環水なら冷水塔の負荷がそれぞれバランスを考えないといけないからです。使用先（ユーザー）が多ければ多いほど、温度差設定をバラバラにしてしまうと複雑になるので、温度差を固定化できるように流量を決めていくという方法がスマートだと思います。
口径の計算
流量m2が決まったら配管口径を決めましょう。
決め方は標準流速を使うと良いです。
加熱側と冷却側の流量が異なるので、口径も変えることになるでしょう。
ここまでの計算なら簡単だと思います。
プレート式熱交換器(heat exchanger)の総括伝熱係数(U値)
プレート式熱交換器の設計としては総括伝熱係数の確認が必要です。
熱交換装置としての性能を決める大きな要素です。
総括伝熱係数(U値)の設計としては以下の関係式を使います。
熱量＝総括伝熱係数×伝熱面積×温度差
数式としてはQ3=UAΔTとしましょう。
熱量Q3
熱量Q3の計算は簡単です。
Q1=Q2=Q3とするのが普通です。
これは、100L/minの水を30℃から60℃に上げるために必要な最小の伝熱面積を持つプレート式熱交換器を設計する、という問題になりますね。
Q3=3,000L/min
温度差ΔT
ΔTは厳密には対数平均温度差を使います。
しかしこの計算は若干面倒です。
それくらいなら温度差の平均を取っても良いでしょう。
Δt1=45(60,30の平均)、Δt2=85(90,80の平均)なので、
ΔT=Δt2-Δt1=85-45=40℃となります。
真面目に計算する場合には対数平均温度差を使いますが、実務的には算術平均温度差で対応できることが多いです。メーカーに設計を依頼するという方法も良いでしょう。オーナーエンジニアとしては実務上の簡易計算の方がはるかに大事です。
総括伝熱係数U
総括伝熱係数Uは本来なら複雑な計算をします。
ところが実務的には近似値や実績値を使います。
プレート式熱交換器なのでU=10kcal/(m2・min・k)としておきましょう。
細かい計算はメーカーに・・・（以下略）
伝熱面積A
ここまで来たら伝熱面積Aの計算は簡単です。
A=Q3/UΔT=3,000/(10・40)=7.5m2
実際にはこの値から多少の余裕を見て決めることになるでしょう。
伝熱面積が大きい場合は・・・
伝熱面積が7.5m2より大きい場合を考えましょう。
この場合は、求める結果としては問題ありません。
伝熱面積が大きい分だけ、交換できる熱量が大きくなります。
本来は60℃まで上がれば十分だったのに、65℃、70℃と上がる可能性があります。
60℃の出口温度を固定化する場合は、温度によって温水側の流量を調整する制御を掛けることでしょう。
こうして装置のスペックは要求より高めにして余裕を持たせておき、運転条件を調整していきます。
伝熱面積が小さい場合は・・・
伝熱面積Aが小さい装置を付けてしまった場合はどういう風に考えましょうか。
例えば1m2の伝熱面積の場合、交換熱量が伝熱面積分だけ減少します。
どれくらい変化があるでしょうか。
Q3‘=3,000/7.5=400kcal/min
この分だけ、上昇温度が下がると考えます。
30+400/100=30+4=34℃が出口の水温度として考えます。
温水の出口温度も減少します（出口流量を変更しないという前提で）。
90-400/300=90-13=77℃
温度差ΔTの修正をしましょう。
ΔT’=(90+77)/2-(34+30)/2=83-32=51℃
教科書的には繰り返し計算となります。
この計算をしていくと、面倒だなぁ・・・という気になってくると思います。
ΔTが変わってしまうと交換熱量がQが変わってしまいますし、固定化していたU値も本来は変わるはずです。
普通は装置の能力が不足する場合の検討はしないのでしょう。
問題のあった装置の解析のために、運転条件を特定しようとしたら意外と難しい、ということが理解できればいいと思います。
参考
伝熱の知識は機電系エンジニアとしてはとても重要です。
以下のような本を使って勉強することは大事です。
関連記事
プレート熱交換器について詳しく知りたい方は、以下の記事をご覧ください。
断熱は伝熱計算がメインになります。詳しく知りたい方は、以下の記事をご覧ください。
最後に
熱量の公式Q=mcΔtを化学プラントで使う例としてプレート熱交換器の設計を紹介しました。
温度差の仮定・U値との比較など現場ならではの簡易計算を実現するための工夫にも触れています。
真面目に計算しても、運転結果と整合性を取るのは意外と難しいです。
簡易計算で失敗しない答えを速やかに見つけるようになりたいですね。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）
*いただいたコメント全て拝見し、真剣に回答させていただきます。
コメント
総括伝熱係数の解説で、Q1=100*1*(60-30)=3,000kJ/min
としてありますが、Cp=1ということは、Kcal/Kgを使っていると思われます。すると、単位はKJ/minではなくて、Kcal/minが正しいのでは？KJを使うのであれば、１のところは4.186KJ/Kg/Kを使う必要がありそうです。Q1=100*4.186*(60-30)=12558KJ/minとなりそうです。
U=30kJ/(m2・min・k)とこちらの方はKJを使っているので、伝熱面積の計算は4.186倍になると思われます。あるいはU=30Kcal/m2/min/kであれば正しい計算になりますが・・・・。
ご確認ありがとうございます。
3000kcal/minが正しいので修正しました。
Uも10kcal/(m2・min・K)にしています。