タンクなどの重量物をボルト固定するかどうか、判定をするための転倒計算を解説します。
重量物をプラント内で固定するためには、アンカーボルトなどを使います。
ところが、タンクではアンカーボルトを使わずに、地面に置くだけというパターンがあります。
アンカーボルトを付けずに設置していいのかどうかを判定するために、専門の計算が転倒計算です。
屋外タンクの耐震耐風計算の一部ではありますが、概念は広く使えるものです。
基礎を知っていろいろな場面で応用が利くようにしたいですね。
物体モデル
対象となる物体モデルです。
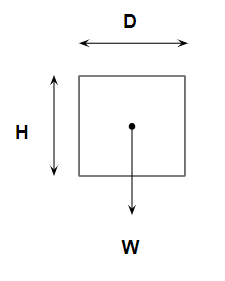
円筒胴のタンクを考えています。
直径D・高さH・重量Wのタンクです。
このタンクの耐震耐風計算とは、地震や台風が起きたときにタンクが移動するかどうかを判定するものです。
アンカーボルトで固定せずに直置きすると、地震や台風でタンクが移動してもおかしくないですからね。
危険物を大量に貯めるタンクだからこそ、移動は避けたいですね。
屋外タンクの場合なら、中に液体が入っていると重りになって移動はしにくくなります。液が入っていることを前提とした設計では、運転時に常に一定の液量を求められることになりますので、やめておきましょう。
地震
地震に対する抵抗性を考えましょう。
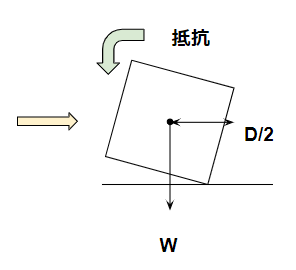
転倒計算をする場合は、物体を少し傾けて1か所で地面と接している状況をイメージしましょう。
地面から浮いているわけではなく、浮きそうになっていて力が作用する部分が1か所という状況です。
転倒しようとするまさに直前はこの条件になっていると考えられます。
転倒モーメント
地震によって物体が転倒する転倒モーメントを考えます。
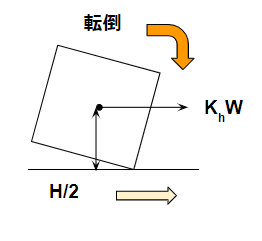
地震によって地面が動いてタンクが動いている時、タンクには水平の力が掛かっていると考えます。
慣性力と同じ考え方で良いでしょう。
これは重量に比例すると考えます。
専門用語で設計水平震度Khという係数を、重量に掛けます。
この値は地域や地盤の状況によって変わります。(1以下です)
地震によってタンクが水平の力を受けていてタンクの重心高さがH/2であるので、タンクが転倒しようとするモーメントを計算できます。
$$ K_hW\frac{H}{2} $$
抵抗モーメント
転倒モーメントとセットで考えるのが抵抗モーメントです。
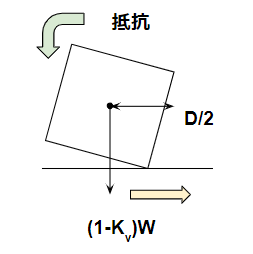
物体が少し浮いたとしても、自重で転倒する方向と逆方向に倒れようとします。
これが転倒に対する抵抗モーメントとなります。
重力はWそのものではなく、ある係数だけ引いた値となっています。
これを設計鉛直震度Kvといいます。
$$ K_v = \frac{K_h}{2} $$
転倒モーメントの計算を振り返ってみると、重量Wのうち水平方向にKh・垂直方向に1-Kh/2という配分をしていることが分かります。
抵抗モーメントは、自重と半径の掛け算としてのモーメントで決まります。
$$ (1-K_v)W\frac{D}{2} $$
判定
転倒モーメントと抵抗モーメントの大小関係を判定します。
転倒しないようにすることが目的なので、
転倒モーメント < 抵抗モーメント
となっていればいいわけですので、判定式は以下のようになります。
$$ K_hW\frac{H}{2} < (1-K_v)W\frac{D}{2} $$
少し変形して、
$$ \frac{H}{D} < \frac{1-{K_h/2}}{K_h} $$
これはタンクの概形を決めるための大きな制約条件になります。
例えば、Kh=0.2としたときには右辺=0.45となるので、アンカーボルトを付けない場合にはタンク高さHはタンク径Dの0.45倍以下にしなければいけないことになります。
直感的に背が高いタンクほど転倒しやすいので、分かりやすいでしょう。
FRPタンクのような大型の水系タンクであれば、この条件を満足することはできません。
この場合には素直にアンカーボルトを付けましょう。
風圧
風圧に関する転倒計算も同じように考えましょう。
転倒モーメント
転倒モーメントは、タンクが風の力を直接受ける状況を考えます。
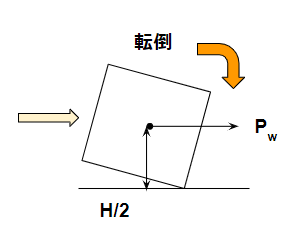
イメージしやすいでしょう。
風の力は圧力×面積で決まります。
風の圧力は風力係数とタンク高さの平方根で決まる値。
風を受ける面積はタンク高さH×タンク径Dで決まる投影面積。
まとめてPwという文字でおいておきましょう。
転倒モーメントは地震の時と同じ発想になります。
$$ P_W\frac{H}{2} $$
抵抗モーメント
抵抗モーメントは地震の時と同じ発想です。
地震の時のような自重の配分は考える必要がなく、全自重が抵抗モーメントとして寄与します。
$$ W\frac{D}{2} $$
判定
地震の時のように判定しましょう。
$$ P_W\frac{H}{2} < W\frac{D}{2}$$
以降の計算は省略します。
アンカーボルト(bolt)が必要な場合
転倒計算をしてアンカーボルトが必要になった、場合も見ておきましょう。
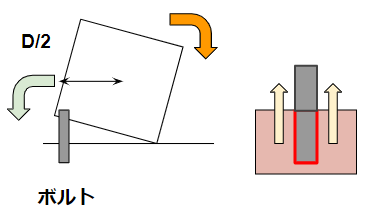
ボルトはタンクの周囲に数本付けることが普通ですが、1本にだけ集中して効くと考えると安全側です。
ボルトを付けることで抵抗モーメントが、増加する方向になります。
アンカーボルトが負担すべき力をFとすると、Fによる抵抗モーメントは
$$ F\frac{D}{2} $$
となります。
$$ P_W\frac{H}{2} = W\frac{D}{2} + F\frac{D}{2}$$
として力Fが決まります。
アンカーボルトはコンクリートに付着して摩擦力として寄与するため、
(ボルトの周長)×(ボルト埋め込み長さ)×(コンクリート付着力) = アンカーボルト引き抜き力
として決まります。
ここから、ボルトサイズを決定します。
参考
プラントの設計では強度計算など高校物理や材料力学の範囲がかなり多いです。
強度計算については以下のような本が参考になります。
関連記事
さらに知りたい方は、タンクのボルト固定に関連する以下の記事をご覧ください。
最後に
タンクなどでボルト固定をするかどうかを判定するための耐震耐風計算の考え方を紹介します。
転倒モーメントと抵抗モーメントの2つを判定します。
地震の時は自重が転倒と抵抗に配分して計算します。
風の時は風圧力の計算をします。
抵抗モーメントが不足している場合は、アンカーボルトが必要でコンクリート付着力を使います。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。(コメント欄はこの記事の最下部です。)
*いただいたコメント全て拝見し、真剣に回答させていただきます。


コメント
タンクの転倒について調べていたところ、こちらのサイトに辿り着きました。
こちらの例ではすべてタンク本体となっていますが、レグ脚がついたタンクでは転倒モーメントと拮抗モーメントの関係はどうなるでしょうか?
コメントありがとうございます。
考え方は重心が高くなるだけですが、関連する情報がありますので、1つ記事にします。