振動について解説していきます。
振動というのは地震の話として話題になることも多いでしょう。
これは区別して震動と呼ぶ場合もあります。
振動でも震動でも物理的な原理は割と簡単ですが、掘り下げると機械系の大学や大学院の専門的な分野になります。
力学の応用的な話で、物が動くところ全てに振動が発生すると考えましょう。
化学プラントの設備でも動きを伴う設備(動機器)はいっぱいありますので、何かあった時の知識としては知っておいた方が有利に働くこともあるでしょう。(頻度は少ないですけど)
それなりの大学の大学院で振動の研究をした私が、過去の記憶だけで化学プラントの機械系エンジニア向けに記載した記事です。ポイントを絞っています。
振動モデル
今回は一自由度の減衰なしの振動について解説します。
モデルとしては以下のようなものを考えます。
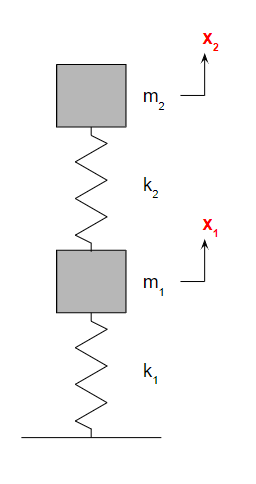
このモデルで登場する記号は以下の意味を持ちます。
- \(m\):質量(kg)
- \(k\):ばね定数(N/m)
- \(x\):変位(m)
質量\(m\)はいわゆる重さのことと考えればOKです。
ばね定数は物理的には「変位に比例する復元力」という意味になりますが、その辺は省略してOKでしょう。
最初は、図のような分かりやすいばねをイメージすると良いです。
ばねの上に重りが載ってある例は、分かりやすい振動系です。
変位\(x\)は質量\(m\)の稼働する方向を示します。
ここでは上下方向にのみ移動する一方向のみの運動という一番簡単なモデルを考えるので、一自由度と呼びます。
【脱線】この絵の通りの、質量とばねを繋げただけの作りで、一自由度振動系を作るのは実は相当難しいです。いわゆるコイルばね(巻きばね)で一方向だけ動くことはなく、x・y・zの3方向や、回転の運動など様々なモードで運動します。振り子とか梁とかの方がよっぽど楽ですね。
運動方程式(外力なし)
振動工学では運動方程式が登場します。
運動方程式とは高校物理で学んだあれです。
$$ ma=F $$
\(a\)は加速度のことです。単位時間あたりの速度変化というもの。
速度は単位時間当たりの変位変化であって、速度を\(v\)とおいたとき、
\(x\)(変位) → \(v\)(速度) → \(a\)(加速度)
というように変位・速度・加速度は時間変化の関係にあります。
これは微分の世界。
$$ v = \frac{dx}{dt} $$
$$ a = \frac{dv}{dt} = \frac{d^2x}{dt^2} $$
という関係になります。
一般にはライプニッツ記法を使わずに、ドットを使ったニュートン記法を使います。
$$ v = \dot{x}$$
$$ a = \ddot{x}$$
この記法を使うと運動方程式は以下のように記載します。
$$ m\ddot{x} = F $$
振動の世界では復元力が大事です。
ばね定数\(k\)、変位を\(x\)としたときに、\(-kx\)で表現されるのが復元力。
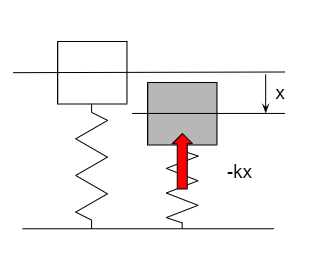
質量\(m\)に関する運動方程式を立てるとき、ばねの復元力\(-kx\)だけが加わっていると考えると、
$$ F = -kx $$
となるので、運動方程式は
$$ m\ddot{x} = -kx $$
となります。振動の世界では特に、以下のように表現することが多いです。
$$ m\ddot{x}+kx = 0 $$
この表現はとてもよく見る振動の基礎式ともいえる表現です。
運動方程式の解き方
この運動方程式の解き方をざっくり解説します。
こうやったら何となく上手いこと解けるという程度に、理解していれば良いと思います。
$$ x = Xe^{iωt} $$
と置き換えます。
これはフーリエ変換という世界の話になりますので、細かい話は省略します。(制御工学ではラプラス変換の世界ですね。)
答えが三角関数になるはずだと予め想定してしまっています。
\(e\)は自然対数の底、\(i\)は虚数、\(ω\)は角振動数、\(t\)は時間です。
何のこと?と思うかもしれませんが、以下のサインカーブだと思えばOKです。
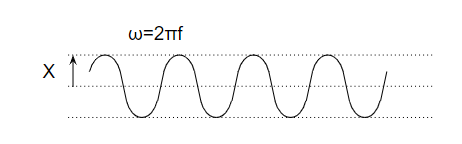
\(X\)は振幅の最大値、周波数\(f\)のサインカーブです。
これを虚数を使って表現すると、解きやすいというだけです。虚数の意味は考えないようにしましょう。
さて、このxを微分すると以下のようになります。
$$ \dot{x}=iωx $$
$$ \ddot{x}=(iω)^2x=-ω^2x $$
これを使うと運動方程式は以下のように表現できます。
$$ (-mω^2+k)Xe^{iωt}=0 $$
この式だけを見ると\(X=0\)となります。
外力が働かない状態では、初期条件として平衡状態からズレた状態でない(安定した状態)だと、動きません。
ここに初期条件として、\(t=0\)での変位や速度を与えると解を得ることができます。
この外力なしの条件は、あまり興味がない部分ですので省略しましょう。
外力なしの場合は、わざわざ虚数を使うよりは\(x=Xsin(ωt+α)\)の形で解く方が良いです。初期条件を変位で与える場合は、\(X=F/k\)、\(α=0\)、速度で与える場合は、\(Xω\)が初速、\(α=π\)の形になります。虚数を使った表現は、どちらかというと以降の展開のためという位置づけが強いです。
運動方程式(外力あり)
これまで外力なしの運動方程式を見てきましたが、いよいよ外力ありのケースを見ていきましょう。
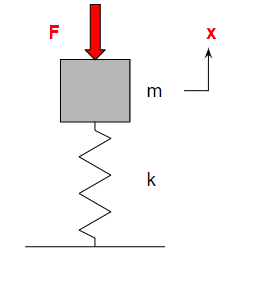
外力って何?と思うかもしれませんが、いろいろあります。
モーターの力・流体の流れ・粉体の落下・地震・台風・・・
化学プラント的には一般的には動機器内で発生する周期的な力が課題になるので、モーターの力を考えても良いと思います。
そういうわけでもありませんが、外力\(F\)は一般に以下の表現をすることが多いです。
$$ Fe^{iωt} $$
運動方程式を解くときに出てきた表現と同じです。
絶対値Fの力で周期的に変動する力という意味です。
これがある角振動数\(ω\)で変化する力だと考えて解きます。
$$ (-mω^2+k)Xe^{iωt}=Fe^{iωt} $$
$$ X=\frac{F}{-mω^2+k} $$
ここで
$$ ω_0=\sqrt{\frac{k}{m}} $$
$$ X_0=\frac{F}{k} $$
とおくと
$$ X=X_0\frac{1}{1-(\frac{ω}{ω_0})^2} $$
この式はとても大事です。
この\(ω_0\)は固有振動数と呼ばれる超重要な用語です。
質量\(m\)とばね定数\(k\)だけで決まります。
対象としている系が決まれば自動的に決まる固有の値です。
\(F\)と\(k\)も固有の値となりますが、求めるべき\(x\)は角振動数\(ω\)に依存する値となります。
ここが振動工学のポイントです。
横軸に\(ω\)、縦軸に\(X\)を取ってみましょう。
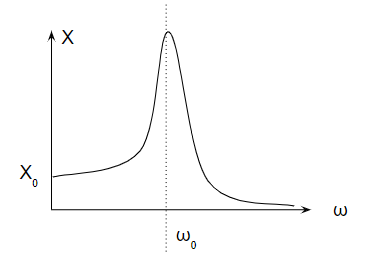
- \(ω=0\)の時、\(X=F/k\)
- \(ω=ω_0\)の時、\(X→∞\)
- \(ω→∞\)の時、\(X→0\)
こんな関係性になります。
大事なのは2の\(X→∞\)になるときのこと。
共振という現象です。
外力の角振動数が物体の固有振動数と等しい時、物体の振幅は無限に大きくなります。
震動という地震の世界では振幅\(X\)を低くする方向に考えることが多いですが、振動という機械の世界では若干その割合は変わります。
とはいえ、共振を起こす振幅が大きくなる現象は、設備を破壊したり危険な方向に行くと考えて良いでしょう。
運転で発生する外力が固有振動数と重ならないように運転することが、振動上は大事
といえます。
上記の\(ω-X\)の関係を周波数応答と呼びます。制御工学のボード線図でも同じ考えが出てきますね。
一方で時間応答という表現がありますが、これは\(x\)そのもの。
一応記載してみると、
$$ x = Xe^{iωt} = X_0\frac{1}{1-(\frac{ω}{ω_0})^2}e^{iωt} $$
となります。
時間\(t\)の情報はサインカーブの形としてだけ登場して、振幅\(X\)には出てきません。
参考
関連記事
最後に
化学プラントの機械系エンジニア向けに振動工学の基本である一自由度振動系の運動方程式を解説しました。
フーリエ変換を前提とした表現があるので、最初はそんなものか・・・と思う感度だと思います。
固有振動数や周波数応答という概念が独特ですので、この概念を知っているだけでも十分だと思います。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。(コメント欄はこの記事の最下部です。)
*いただいたコメント全て拝見し、真剣に回答させていただきます。


コメント