振動(vibration)について解説していきます。
2自由度振動系です。
1自由度の振動系があれば、当然のように2自由度の振動系があってもおかしくないですよね。
単に「1」が「2」になっただけでは。
そう思うかもしれませんが、内容はグッと深くなります。
この辺りになると、化学プラントの機電系エンジニアとしては普通は使いません。
化学系の学部の人が、機械系の学部は「工具触って自動車いじるのでしょ?」という思い込みをしがちですが、そうではないですよというアピール目的ですかね。
2自由度振動(vibration)系のモデル
2自由度の振動系のモデルを見ていきましょう。
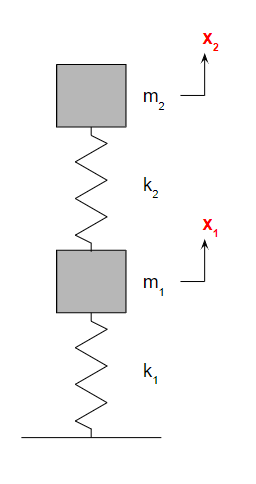
2自由度振動系は、1自由度振動系を2つ重ねたような形をしています。
質量\(m\)・ばね定数\(k\)・変位\(x\)で構成されるシステムです。
添え字の1,2を付けて区別しましょう。
1自由度振動系の記事でも書きましたが、この絵の通りのコイルバネと重りで2自由度系を作ろうとすると相当大変ですよ。
運動方程式
2自由度振動系の運動方程式を考えましょう。
前提として、外力\(F\)は\(x_1\)側にのみ掛かっているとします。
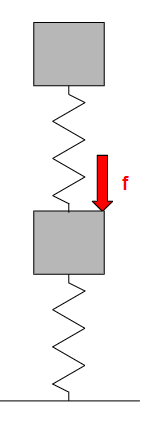
運動方程式は\(x_1\)、\(x_2\)に対して立てましょう。
$$ m_1\ddot{x_1}+k_1x_1 = f+k_2(x_2-x_1) $$
$$ m_2\ddot{x_2} = -k_2(x_2-x_1) $$
ばねの復元力の方向は間違えないようにしましょう。
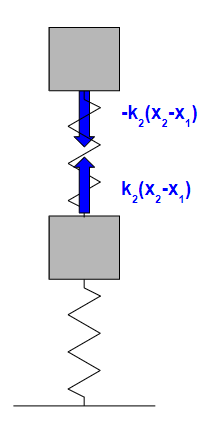
\(x_2\)が\(x_1\)よりも+方向に大きく動く場合に、ばね\(k_2\)は伸びて、縮まろうとする復元力が働きます。
その時の復元力の働きが上の図の通りとなります。
\(x_1\)側の運動方程式は1自由度の振動系に、復元力\(k_2(x_2-x_1)\)が外力として加わっていることを意識した表現にしました。
\(k_1\)側のばねの復元力も外力として考えて記載するところから出発する人の方が多いかもしれませんね。
その辺は流儀ということで。
上記の運動方程式を、簡単に変形しましょう。
$$ m_1\ddot{x_1}+(k_1+k_2)x_1-k_2x_2 = f $$
$$ m_2\ddot{x_2}+k_2(x_2-x_1) = 0 $$
運動方程式を解く
1自由度の振動系と同じように運動方程式を解いていきましょう。
$$ x_1=X_1e^{iωt} $$
$$ x_2=X_2e^{iωt} $$
$$ f=Fe^{iωt} $$
と置きます。
$$ -m_1ω^2X_1+(k_1+k_2)X_1-k_2X_2 = F $$
$$ -m_2ω^2X_2+k_2(X_2-X_1) = 0 $$
下の方の式から、\(X_1\)と\(X_2\)の関係が出てきます。
$$ X_1=(1-\frac{m_2}{k_2}ω^2)X_2 $$
この式から\(X_2\)が導け出せます。
$$ (1+\frac{k_2}{k_1}-\frac{m_1}{k_1}ω^2)(1-\frac{m_2}{k_2}ω^2)k_1X_2-\frac{k_2}{k_1}k_1X_2 = F $$
ここで、
$$ ω_1=\sqrt\frac{k_1}{m_1} $$
$$ ω_2=\sqrt\frac{k_2}{m_1} $$
$$ \frac{k_2}{k_1} = φ $$
と置きましょう。
$$ (1+φ-(\frac{ω}{ω_1})^2)(1-(\frac{ω}{ω_2})^2))k_1X_2-φk_1X_2 = F $$
これを変形して、\(X_2\)とさらに\(X_1\)が出てきます。
$$ X_2=\frac{F}{k_1}\frac{1}{(1+φ-(\frac{ω}{ω_1})^2)(1-(\frac{ω}{ω_2})^2))-φ} $$
$$ X_1=\frac{F}{k_1}\frac{1-(\frac{ω}{ω_2})^2}{(1+φ-(\frac{ω}{ω_1})^2)(1-(\frac{ω}{ω_2})^2))-φ} $$
解釈
文字がいっぱい出てきて、結果の式がどういう意味を持つのか考えるのが大変ですね。
これは振動工学のあるあるといえます。
1つずつ見ていきましょう。
φ
\(φ\)は2つのばね定数の比です。
\(φ=0\)の場合は、\(x_1\)は1自由度系と同じ式に戻ります。
\(φ→∞\)とすると、\(k_2\)→∞となって\(X_1=X_2\)となると考えておきましょう。
\(k_1→0\)の場合は、外力Fの動きに合わせて\(X_1\)と\(X_2\)が周期的に動く形になります。
実際にこれらの極端な系を想定することはありませんが、得られた計算式が物理的なイメージとあっているかどうかを検算する癖は大事だと思います。
ですが\(φ→∞\)の方がちょっと苦しいですね。
この考え方は、化学プラントの実務でも多角的な思考と表現されるかもしれません。
\(ω_1\)、\(ω_2\)
これらは\(X_1\)、\(X_2\)それぞれの固有振動数と考えます。
2自由度系ですが、それぞれ単独に切り離した場合の固有振動数をパラメータにしていると便利です。
\(X_1\)
\(X_1\)側には絶大な意味があります。
それは
\(ω=ω_2\)の時、\(X_1=0\)
ということ、
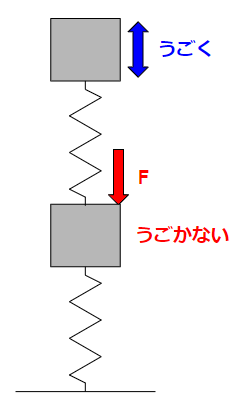
これは\(X_1\)に力を加えても、\(X_1\)は動かずに代わりに\(X_2\)だけが動くということを意味します。
一見、変な気がしますよね。
力を加えた部分が動かないのですから。
これが制振・制震という振動制御の基本となります。
現実的にはゼロにすることはできませんが、\(X_1\)の動きをできるだけ小さくするという考えです。
\(X_2\)
\(X_2\)は周波数応答を考えてみましょう。
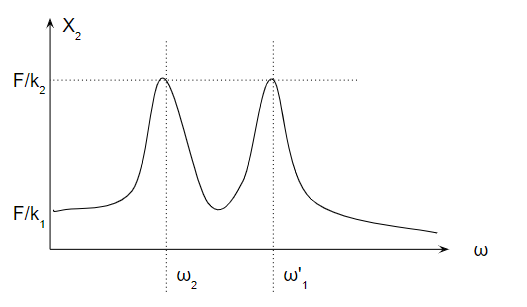
1自由度の時に比べて、2自由度はピークの数が2つになります。
実は、自由度はこのピークの山の数と一致します。かなり大事な考え方です。
\(ω=0\)のときは、\(X_2=F/k_1\)という結果になります。
これは\(X_1\)にゆっくり力を加えると、\(X_2\)は\(X_1\)と同じ動きをして、\(k_2\)の復元力は働かないことを意味します。
\(ω=ω_2\)は1つ目の山のピークです。
このピークとなる角振動数は共振振動数と呼びます。
複数の共振振動数を持つ場合は、振動数の少ない側から1次モード・2次モード・・・と呼びます。
この場合\(ω_2\)が1次モード、\(ω’_1\)が2次モードです。
\(ω=ω_2\)の場合は、\(X_2=F/k_2\)となります。
実は、\(k_1>k_2\)を前提に含んでいます。
\(ω=ω’_1\)は2次モードですね。
$$ ω’_1=\sqrt{\frac{k_1+k_2}{m_1}} $$
が2次モードの共振振動数となります。
整理すると、\(ω’_1>ω_1>ω_2\)という関係があります。
参考
振動は化学プラント的には参考知識ですが、機械系としてはかなりメジャーな分野です。
1冊何か持っていると、トラブルがあった時などに重宝しますよ。
関連記事
最後に
化学プラントの機械系エンジニア向けに二自由度振動系の運動方程式を解説しました。
変数・文字が急激に増えて複雑さが一気に増します。
振動制御という点に着目するとき、自由度を増やして質量とばね定数を適切に定めることが大事だとわかります。
自由度が増えると、共振点も増えていきます。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。(コメント欄はこの記事の最下部です。)
*いただいたコメント全て拝見し、真剣に回答させていただきます。

