モーター電動機のことはとにかく電気エンジニアに任せがちな機械エンジニア。
でもモーター電動機って機械系の知識と密接に関係します。
電圧・電流という単語がある瞬間に遠ざかっていたら、結構もったいないです。
機械設備保全エンジニアならモーターと関わることもあるでしょうが、機械設備設計エンジニアは遠ざかりがち。
そうしていると、ポンプや攪拌機の統合的な理解はいつまで経ってもできません。
どこかのタイミングで本記事の知識は勉強しておきたいですね。
物理的次元
物理的な次元というと、MKS単位が一般的です。
- m:メートル(meter)
- k:キログラム(kilogram)
- s:秒(second)
この次元でなじんでいますが、電動機では電流・電圧という概念があります。
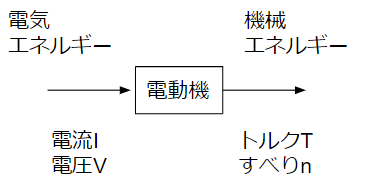
電動機の入力は電流・電圧で議論し、出力がトルク・回転数で議論するため誤解しやすくなります。
仕事・エネルギーで統一
電動機の入力と出力で同じ次元で議論されるパラメータがあります。
それは仕事・エネルギーです。
機械・電気それぞれのエネルギーを変換する装置が電動機。
物理的なエネルギー
物理的な次元ではエネルギーは下記のように表現します。
$$\frac{kg・m^2}{s^2}$$
私は位置エネルギーの定義である、質量\(m\)の物体を重力に逆らって\(h\)上昇させるための仕事
$$mgh$$
からエネルギーの次元をたどっていきます。
運動エネルギーからたどっても良いでしょう。
入力の電流電圧と出力のトルク回転数はJの次元で整理しましょう。
機械の仕事はトルク
機械の仕事はトルクそのものです。
トルク\(T\)とは力×距離ですので、
$$\frac{kg・m^2}{s^2}$$
というエネルギーの次元を持っています。
トルクに回転数をかけると出力になります。
回転数は1/sの次元を持ちますので
機械的なエネルギー = トルク
機械的な出力 = トルク×回転数
という次元関係になります。
電気的なエネルギー
電気の出力は電流×電圧です。
これでkWの単位として表現します。
出力は単位時間当たりのエネルギーですので、エネルギーをW・時間をsという次元であるため、出力は
$$Ws$$
という次元になります。
電気的なエネルギー = 電流×電圧×時間
電気的な出力 = 電流×電圧
という次元関係になります。
トルク×回転数 = 電流×電圧
電気的な出力と機械的な出力はどちらも同じkWの次元で考えます。
そうすると、
トルク×回転数 = 電流×電圧
という関係になります。
ファラデーの電磁誘導の法則
ファラデーの電磁誘導の法則とは以下の通りです。
導体が磁束を切れば、導体に電圧が発生する。
機電系設計者として、高校の物理で触れたこともあるでしょう。
実際にはここまで知っているだけでも十分ですが、もう一歩深堀りして理解してもいいでしょう。
導体とはシャフト
導体・磁束という電気の専門用語を機械用語とすぐに結びつかない人もいるでしょう。
安心してください。
本記事はその電気と機械を結びつけるのが目的です。
導体とはシャフトの事です。
電動機は電気の力を機械の力に変えます。
出力はシャフトの回転力です。
シャフトに電流が流れる
導体であるシャフトが磁界を横切れば、シャフトに電流が流れます。
これは「誘導電流」と呼ばれますね。
シャフトに力が加わる
シャフトが磁界の中にあり、シャフトが動くと、シャフトに電流が流れます。
磁界の中にあるシャフトに電流が流れると、シャフトに力が加わります。
これはいわゆる電磁力です。
この電磁力が回転力という出力になります。
磁界の発生方法
ここまで、シャフトに視点を当ててみていきました。
ところが、磁界に関する話の方が重要です。
導体と磁界がセットで、力が生み出せます。
この方法が2種類あり、キャンドポンプとマグネットポンプの差になります。
キャンドポンプ
磁界の発生方法は2種類あります。
- コイルに交流の電流を流す。
- 磁石を物理的に動かす
コイルに交流の電流を流すということは、コイルに電流の変化を与えるということです。
コイルに電流の変化が生じると、コイルに磁界が発生します。
この原理を使用したのがキャンドポンプ。
誘導電動機もこの原理を使っています。
キャンドポンプとは誘導電動機をそのままポンプにした構造です。
交流の電源として、変電所からの交流電源が使えます。
コイルの中にシャフトを入れ、コイルに交流電源を流すと、シャフトが回転する
これが誘導電動機の原理です。
マグネットポンプ
磁界の発生方法の2つ目に、磁石を物理的に動かすという方法があります。
マグネットポンプはこれを利用しています。
磁石を動かすと、磁界が変化します。
磁界が変化すると、磁界内にある導体に電流が流れます。
磁界が変化し、電流が流れるので、シャフトの回転力という力が発生します。
- マグネットポンプ 交流電流 → 電動機のシャフトを回転 → シャフトに繋がった磁石が回転 → ポンプのシャフトが回転
- キャンドポンプ 交流電源 → ポンプのシャフトが回転
同期速度・すべり・トルクの定義
誘導電動機で大事な同期速度・すべり・トルクの定義を紹介します。
同期速度 Ns
同期速度は、極数・周波数で決まる数字です。
$$ N = 120×f/P $$
- fが周波数で関西なら60Hz
- Pは極数で4Pモーターなら4です。
つまり、60Hz,4Pのモーターなら同期速度は1200×60/4 = 1800 rpmと決まります。
これが電動機の固定子で発生する、磁界の変化速度です。
すべり s
すべりとは、固定子の磁界変化速度と回転子の物理的な速度差のことです。
固定子は動きませんので、物理的な速度はゼロです。
回転子は物理的な速度を持ちます。
しかし、この物理的な速度差を見ても意味がありません。
回転子の回転速度が速いほど、固定子と回転子の間の相対速度は速くなるだけです。
固定子で磁界が変わると、その磁界の変化につられて、回転子中の磁界が変わり、回転子に電流が流れます。
回転子の磁界と電流によって、回転子は回転をします。
ここで、固定子の磁界が変わる速度と、回転子の回転速度が全く同じ場合
固定子がどれだけ磁界を変えても、その磁界変化を回転子が受け取ることはできません。
回転子の方が固定子よりも微妙に速度が遅く、固定子の力に引っ張られる形で回転子は動きます。
「誘導電動機が電気の力で機械を動かす」という原理から考えても、固定子である電気の力が回転子の機械的な力に変換されるというのは当然のこと。
この辺を教科書では、同期速度Nsと回転子速度Nという表現で説明しています。
すべりはsで表記します。
- s=1 回転子が動いていない
- s=0 回転子と固定子の速度が等しい
トルク T
誘導電動機の機械的出力Pは回転子の速度NとトルクTに対して下記の関係があります。
$$ P ∝ N×T$$
次元の比較もしましょう。
$$ 左辺 = kW = kJ/S = N・m/s $$
$$ 見辺 = 回転速度(1/s)×トルク(N・m) = N・m/s $$
次元は同じですね。
回転速度は同期速度Nsとすべりsを使って
$$ N = Ns × (1-s)$$
という関係がありますので、電動機の機械的出力Pは
$$ P ∝ Ns×(1-s)×T $$
という関係が出てきます。
- s=1 回転子が動いていない → 出力Pはゼロ
- s=0 回転子と固定子の速度が等しい → 出力Pが最大
すべり・トルクの関係
すべりとトルクは直結の関係にあります。
トルクという単語は機械エンジニアにもなじみのある単語です。
ところが、すべりはモーターの用語。
なじみがあまりないのが普通です。
すべりの定義を知ったところで終わり。
という人が多いと思います。
でも、すべりとトルクは密接な関係にあります。
すべりは回転子での損失
すべりとは回転子での機械損失と言い換えることができます。
回転子の入力を1、すべりをsとした場合、回転子の入力:回転子の損失:回転子の出力=1:s:1-sという関係が成立します。
s=1なら回転子は動かず、s=0なら回転子は固定子と同じ速度という定義ですので、
- 回転子が動いていないs=1では、全てが回転子の損失
- 回転子が固定子と同じ速度で動くs=0では、回転子の損失がゼロ
という関係性になります。
ポンプには様々な効率係数がある
ここで機械エンジニアがポンプを議論するときに、出てくる効率の話を少しします。
ポンプでの効率というと、
(ポンプの出口で発生する流量×揚程) / (ポンプに加える電流×電圧)
という機械エネルギー/電気エネルギーを効率と定義しています。
これはポンプシステムを俯瞰してみた場合、インペラに着目した思想です。
インペラでのエネルギー損失を効率と言い換えていると言っても良いでしょう。
この他の損失としては、ベアリング・継ぎ手・モーターなどがあります。
このモーターでのエネルギー損失の一つが回転子での損失であり、すべりと言われます。
すべりとトルクの関係イメージ
すべりとトルクの関係は一般に下図のようになります。
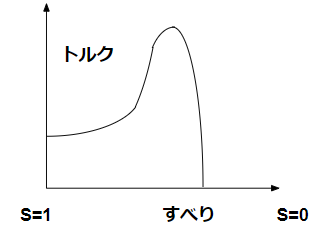
トルクはすべりに反比例ではない
トルクとすべりは主力に対して
$$P∝N_s(1-s)T$$
という関係がありますので、
s=1の時がトルクが最大で、s=0でトルクがゼロになる
と誤解するかもしれません。
というのも、上の式を変形すると
$$T∝\frac{P}{1-s}$$
という関係になるからです。
1/(1-s)という部分だけを見ると
s=1の時がトルクが最大で、s=0でトルクがゼロになる
という部分とずれがありません。
出力にもすべりが影響する
ところが、出力Pにも当然ながら、すべりの要因が乗ってきます。
すべりがあるということは回転子の速度が変わり、
回転子の速度が変わるということは、電動機の出力速度が変わるということ。
電動機の出力は電流×電圧で決まりますが、
電流は電圧/抵抗です。
抵抗は出力速度に影響しますので、電流は出力速度の影響を受け、出力が出力速度の影響を受ける。
だからこそ、出力Pがすべりに影響があるというロジックです。
トルクとすべりの関係
出力とすべりの間にはすべりが小さい方が出力が大きいという
$$P∝\frac{1}{s}$$
の関係が整理湿します。これを先の式に代入すると、
$$P∝\frac{1}{s(1-s)}$$
という関係が得られます。
これを詳細に書いたのが、上の図です。
s=0より少し大きい値で最大値を取る
という関係が出てきます。
速度制御
そもそも速度制御は何のために行うでしょうか。
電動機自身は速度は一定です。
この速度のまま、運転できる機械とそうでない機械があります。
ポンプであれば、モーターの回転数そのままでインペラを回す設計をしています。
ところが攪拌機に、モーターと同じ回転数で運転しようとしたら、負荷が高すぎるケースが多いです。
バッチ系化学プラントでは、速度制御は基本的には減速を目的としています。
減速機も速度制御
電動機そのものに着目しているとイメージしにくいですが、減速機は立派な速度制御です。
今回のテーマからは外れますが、減速機は機械屋として重要な装置ですので。最初に挙げました。
インバータは速度制御の王道
速度制御の王道はこちらです。
電圧周波数を変換する仕組みです。
バッチ系化学プラントでインバータを使う例をいくつか紹介します。
ポンプでインバータ制御は難しい
ポンプでインバータを付けるというのは、かなり限定的です。
ポンプで速度を下げると、流量が下がる以上に、揚程が下がります。
揚程が下がった瞬間に、送液できなくなります。
ポンプメーカーなどでインバータを推奨する会社もありますが、ポンプメーカーは一般論でしか案を提示できません。
彼らがインバータを推奨する前提として運転条件を的確に把握という表現を使います。
バッチ系化学プラントのように生産品目が変わり、運転条件がランダムに変わる場所ではポンプにインバータ制御は使えない、という判断をできるかどうかがエンジニアにとって重要です。
バッチ系化学プラントでは、流量が極めて少ないポンプなど、非常に限定的な場面でしか使えません。
撹拌槽ではインバータ制御は簡単
撹拌槽ではインバータ制御は容易です。
インバータ制御をすると、撹拌速度が変わります。
撹拌槽内の撹拌性能は、攪拌機の速度で決まります。
ポンプのように揚程に影響が出るわけでなく、単純に撹拌性能にのみ影響が出ますので、撹拌槽はインバータ制御が容易です。
特にバッチ系化学プラントでは、生産品目によって運転条件が変わるのが普通ですので、反応を行う撹拌槽はインバータを付けるのが普通です。
ある製品では反応を行い、別の製品では反応を行わないというような撹拌槽があった場合にも、インバータを使います。
完全に反応を行わない目的の撹拌槽に限って、インバータを付けないという発想になります。
バッチ系化学プラントでは、生産品目が変わっても、特定の装置で特定の処理工程を行うことは普通ですので、インバータの要否をそこで限定しています。
その他の制御
インバータが速度制御の基本ですが、他の方法を見ましょう。
極数変換
極数変換は原理的には速度制御の1つです。
同期速度\(Ns\)は
$$N_s=\frac{120f}{P}$$
であり、インバータがfを変えるのに対して、極数変換はPを変える思想です。
実はあまり接したことのない方法です。
V/f一定制御、すべり周波数制御、ベクトル制御
これは周波数制御の1種です。
インバータ制御が一般的な現在ではほとんど使わないでしょう。
電圧・周波数の変化
誘導電動機を入出力という面で見ると、入力は電気の力・出力は機械的な力です。
電気の力として、電気の仕様を示す電圧と周波数が2大指標となります。
インバータをVVVFといいますが、これは
Variable Voltage Variable Frequencyの略であり、電圧と周波数を変えることをVVVFと言います。
VVVFで電圧や周波数を変えた電気の力を入力として、誘導電動機は機械的な出力を変更します。
VVVFが無くても電圧周波数は微妙なブレがあります。
このブレによる電動機出力の各種指標がどういう影響を受けるか見ていきます。
電圧の変化による影響
電圧は定格電圧の±10%以内の変動では、実用上の影響が出てはいけないとJISで定められています。
電圧が低い側、つまり定格電圧の90%となったときに、どうなるかを以下で確認します。
電圧が高い側は、低い側の逆とほぼ考えればいいと思います。
トルクは20%ほど下がる
電圧が下がると、トルクは下がります。
10%電圧が下がると、トルクは20%くらい下がります。
トルクは電圧の2乗に比例するからです。
仕事率 = トルク × 回転数 の関係があります。
仕事率は出力そのものであり、電流 × 電圧 と同じ次元。
電流は 電圧 / 抵抗 なので、出力であるトルクは電圧の2乗に比例します。
周期速度は変わらない
周期速度は周波数に依存するだけで、電圧には依存しません。
すべりは20%ほど上がる
電圧が下がり出力が小さくなるということは、すべりが大きくなります。
すべりとは回転子での損失そのもの。
出力が小さくなるということは、その分が損失となります。
出力はすべりの2乗に反比例するオーダーなので、トルクの出力に対する関係とすべりの出力に対する関係は逆の関係になります。
負荷速度は1%ほど下がる
出力が下がるため、速度も下がります。
ただしその減少量は微小です。
負荷電流は10%ほど上がる
これはちょっと意外に感じるかもしれません。
出力が下がると電流も下がりそうなイメージがあるからです。
電動機の出力Pは以下の関係式で定義されます。
$$P =√3IVcosΦ$$
Iは電流、Vは電圧、cosΦは力率です。
電圧Vが下がっても、出力Pを低下させないようにするために、電流Iがカバーするという現象が起きます。
これは電圧の減少量が低い領域でのみ成立します。
電圧がもっと下がれば結果は変わります。
周波数の変化による影響
周波数は定格周波数の±5%以内の変動では、実用上の影響が出てはいけないとJISで定められています。
周波数が低い側、つまり定格周波数の95%となったときに、どうなるかを以下で確認します。
周波数が高い側は、低い側の逆とほぼ考えればいいと思います。
トルクは10%ほど上がる
周波数が下がると、トルクが上がります。
仕事率 = トルク × 回転数
の関係性ががあり、回転数は周波数でそのまま決まるからです。
周波数の下がりが少ない領域では、仕事が変わらないようにカバーしようとする動きがあり、回転数が下がった分を、トルクがカバーするという構図ができます。
同期速度は5%ほど下がる
同期速度は周波数そのもので効きます。
$$N = \frac{120f}{P}$$
この関係式のそのものです。
すべりは変化なし
すべりは周波数が変わっても影響がありません。
速度自体は下がりますが、入力である同期速度が変わった分だけ、出力である回転子の速度は落ちます。
結果、すべりは変わらないです。
負荷速度は5%ほど下がる
すべりが変わらないけど同期速度が変わるので、その分だけ負荷速度は下がります。
負荷電流はやや下がる
負荷速度が下がれば、電流も下がります。
これは数値的には表現が難しいです。
電動機の負荷
電動機は電気の力を機械的な力に変えて、ある対象物にその機械的な力を与えます。
この機械的な力を「負荷」と言います。
電動機は、負荷対象物に負荷を加える、という言い方をします。
この負荷は、機械の種類によって約3種類に分けれます。
速度依存トルク
速度依存トルクはポンプ・送風機・撹拌機などが該当します。
バッチ系化学プラントのほぼ全てですね。
負荷対象物の速度が上がると、トルクが上がります。
負荷対象物である流体は、
- 速度に比例して抵抗力があがる
- 電動機から発生する回転モーメントが、流体の運動量に転換される
という物理的解釈からもイメージできます。
トルク\(T\)の定義が力\(F\)と距離\(r\)を使って
$$T=Fr$$
と表現され、
出力\(P\)の定義が回転速度\(ω\)を使って
$$P=Tω$$
と表現されることから、
回転速度が上がり、トルクも同じように上がると、出力は速度の2乗・3乗で上がります。
速度依存の負荷では、回転数とトルクが比例関係にある!
定トルク
有名な例がベルトコンベアですが、バッチ系化学プラントでは目にする機会が少ないでしょう。
バッチ系化学プラントではホイストクレーンなどが該当しますが、これを意識する人はほとんどいません。
ベルトコンベアではベルトの送り速度を変えても、運ぶ重量物は変わらないでしょう。
ホイストクレーンも一定の重量を釣り上げていますが、速度が違うだけです。
速度が変わってもトルクが変わらないため、出力\(P\)は速度\(v\)に比例します。
定トルクの負荷では、回転速度かかわらずトルクは一定!
定動力
これは巻き取り機などが該当します。
巻き取り機などでは、巻き取り開始時は半径が小さく、巻き取り終盤では半径が大きくなります。
巻き取り速度を変えてしまうと、巻き取り機に送る原料速度を変えないといけなくなり、運転管理も難しくなります。
巻き取り開始時も終盤も同じ速度で巻き取れるようにするためには、
巻き取りが進むにしたがって、回転速度が下がり、トルクを上げなければいけません。
これは出力を一定にするということを意味します。
定動力の負荷では、動力は常に一定!
参考
最後に
機械エンジニアも関係があるモーターの知識を解説しました。
物理的次元・ファラデーの電磁誘導・すべり・電圧周波数の変化・電動機の負荷
モーターは電気のものだから理解を諦める機械エンジニアも多いですが、上で述べた知識は是非とも知っておきたいです。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。(コメント欄はこの記事の最下部です。)
*いただいたコメント全て拝見し、真剣に回答させていただきます。


コメント