材料力学(material mechanics)について解説します。
材料力学は機械系大学生の基本科目。
どこの製造業でも使えそうな学問です。化学プラントも例外ではありません。
この学問をちゃんと知っているかどうかは、応用力に関連します。
材料力学は範囲が広く計算が多いイメージですが、その辺はできるだけ省略して、特に使う部分だけに絞りに絞って解説します。
専門用語
材料力学では何の断りもなく塑性とか脆性などの専門用語が出てきます。
この意味をちゃんと理解できないまま、読み進めないといけないので、理解が遅れがちになる機電系学生も多いでしょう、
化学プラントの機械屋でも材料力学に触れる機会がありますが、専門用語を知らないと困るシーンがいくつかあります。
そこで、材料力学で登場する性質の定義をまとめます。
弾性・塑性
弾性と塑性は材料力学でも基本の概念。
これは定義を説明している教科書も多いでしょう。
私の解釈は以下のとおりです。
- 弾性は力を離すと元に戻る
- 塑性は力を離しても永久に戻らない
輪ゴムを伸ばしても元の位置に戻る程度の変形を弾性変形と言います。弾力があるなんて言いますよね。
ビニール袋を引っ張って伸び切った状態を塑性変形と言います。塑性って英語でplasticityって言います。プラスチックですね。
輪ゴムやビニール袋だとイメージしやすいのですが、金属でも同じように弾性と塑性を議論します。
脆性・もろい
脆性と「もろい」はほぼ同義で使います。
「もろい」ってどういうイメージがあるでしょうか。
朽ち果てたペットボトルなどが、簡単な力ですぐに粉々になるイメージがありませんか。
材料力学の定義もこれとほぼ同じです。
力を加えると変形しないで破壊する
これが脆性と定義です。
力を加えると一般には最初の伸びるモードがあります。
伸びきった後で破壊するモードが起こります。
脆性が高い材料（つまり、もろい材料）の場合は、変形するモードがなくていきなり破壊するモードに移ります。
一般の「もろい」というイメージと違うのは、力の大小ですね。
材料力学でいう「もろい」は力が大きくても変形せずに破壊すれば「もろい」です。
脆性は物体の環境によって変わります。
- 低温脆性 温度が低い炭素鋼はもろくなる
- 常温脆性 リンを多く含む炭素鋼は、常温でもろくなる
- 青熱脆性 炭素鋼は200～300℃でもろくなる
- 赤熱脆性 硫黄を含む炭素鋼が、900℃を越えるともろくなる
- 水素脆性 炭素鋼は水素があるともろくなる
細かい定義は別として、もろくなることは共通しています。
バッチ系化学プラントでは低温脆性と水素脆性に注意すればOKです。
ねばい
「ねばい」は「もろい」の逆として考えればいいでしょう。
弾性変形・塑性変形を問わず変形するモードが強い性質を「ねばい」と言います。
衝撃
衝撃は言葉どおりの意味です。
力の加え方として、以下の2つで性質が大きく変わります。
- ゆっくり力を掛ける
- 衝撃的に力を掛ける
ゆっくり力を掛けた場合には強い材料でも、衝撃的な力を掛けるとすぐに破壊する材料もあります。
化学プラントの材料では、低温で衝撃に弱い性質を示す点が話題になります。
低温脆性と衝撃値が低いことがほぼ1：1でリンクしていると考えて良いでしょう。
バッチ系化学プラントで使う反応器が炭素鋼でできていて、0℃以下の温度で使用するために低温脆性が課題となります。
疲労
疲労は繰り返し力を掛けるときに話題になります。
針金を何度も曲げると折れますよね。
これは疲労です。
弾性限度以下の弱い力で破壊しない材料でも、繰り返し力がかかることで破壊します。
疲労破壊は化学プラントではどこでも発生する怖い現象です。
目に見える動きがない化学プラントでも、疲労破壊を起こす程度の動きは起こります。
クリープ
クリープは力を掛けた状態で時間を掛けつづけるとひずみが増える現象です。
普通は応力ひずみ関係が決まっていれば、応力が変わらなければ時間に関係なくひずみは一定のはずです。
これが時間が経ては勝手にひずんでいくのがクリープです。
特に高温の材料で話題になります。
応力ひずみ関係
応力ひずみ関係について紹介します。
応力ひずみは材料力学の基本です。
「ひずみ」とは日常的に使う用語の一つですが、材料力学上は違います。
整理していきましょう。
応力の定義
外力と内力という使い分けをします。
外力とは言葉どおり外から加わる力、内力は物体内部で働く力です。
下の図のように、細長い棒に外からPの力を加えて引っ張ったとしましょう。
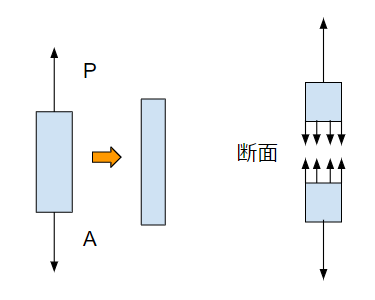
このPは外力と言います。
外力Pを受けて、棒は伸びます。
この棒が伸びているとき、棒の内部では力の伝達が起きています。
棒内部のある点を切った断面を見てみましょう。
断面を境に2つの部材に割ったとき、外力とバランスするように内力が働いていると考えます。
内力は内部に働く力なので、断面前後の内力は同じ力です。
外力と内力も当然ながら同じ力です。
磁石のN極・S極を2つに割ったら、断面でN極・S極ができあがるのと同じことです。
応力の定義は以下のように表現できます。
$$σ=\frac{P}{A}$$
圧力の定義もこれと全く同じです。
圧力は外力が働く断面に掛かる応力と考えると良いでしょう。
上の例は垂直応力と言います。
応力の働く面と応力の働く方向が垂直関係にあるからです。
垂直の反対はというと並行ですよね。
応力の働く面と応力の働く方向が並行関係にあるものをせん断応力と言います。
下の図のとおり。
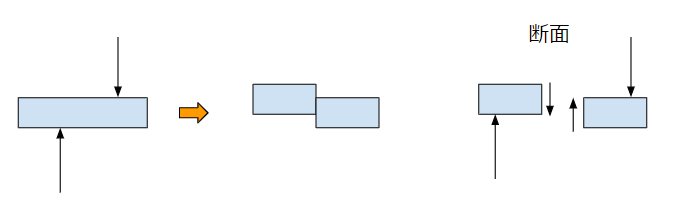
細長い棒をモデルとして考えましたが、現実世界には3次元的に考えて、
3つの垂直応力と3つのせん断応力が掛かる複雑な現象です。
これを簡略化して、現実の構造物の強度設計を行います。
ひずみの定義
ひずみは応力を受けて伸びた量です。
細長い棒の例をもとに解説します。
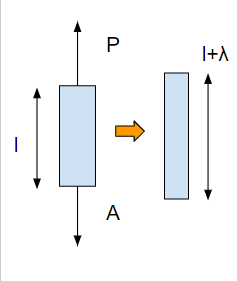
ひずみは変形した量を無次元化したものというのが定義です。
伸びる前の長さlに対して、伸びた後はl+λになったとしましょう。
この伸び量はλです。単位はmやmmなど長さの単位です。
ひずみはこれを無次元化した以下の定義になります。
$$ε=\frac{λ}{l}$$
応力ひずみ曲線
応力とひずみは一定の関係があります。
フックの法則
バネをモデルに考えた時、ばね定数をkとすると
$$P=kλ$$
と書くことができます。
$$σ=k\frac{l}{A}ε = Eε$$
この式は応力とひずみが係数Ｅに比例するという関係です。
このEをヤング率や縦弾性係数と呼びます。
これは材料に固有の定数です。
この関係はフックの法則と言います。
上の式では先にばね定数をkとして与えていますが、実際は逆です。
ヤング率Eを使って、ばね定数kを
$$k=E\frac{A}{l}$$
と表現する方が普通です。
同じ材料でも断面積が大きいほど、長さが短いほど、ばね定数が高いです。
これはつまり「硬い」ということですね。
応力ひずみ線図
応力とひずみの関係は以下のような関係があります。
複雑ですね
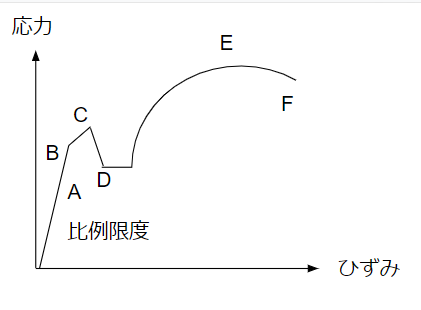
A～Fまでポイントがあります。
- A：比例限度
- B：弾性限度
- C：上降伏点
- D：下降伏点
- E：破壊点
- F：破断点
それぞれの点の説明をしましょう。
A：比例限度
応力が加わると材料はどんどん歪んでいきます。
応力を取り除くとそのひずみは除去されます。
バネやゴムをイメージすればいいでしょう。
応力ひずみの関係は最初は線形近似ができます。この限界点がA。
ここまでは、\(σ=Eε\)の関係が成立します。
B：弾性限度
応力を取り除くとひずみは除去されます。
ところが応力が強すぎると、ひずみを除去しても完全に元には戻りません。
半透明のビニール袋を伸ばしていくと、途中で白くなりますよね。
ここまで引っ張ると、力を除いても変形が残ったままになります。
この限界点を弾性限度といいます。
比例限度から弾性限度までの間は、フックの法則は成立しませんが、
力を取り除くと元の位置に戻ります。
C：上降伏点
降伏点はこれ以上力を増やしていくと、力を増やさなくても勝手にひずみが進んでいきます。
降伏点に一度到達すると、複雑な応力ひずみ関係でしばらく推移します。
この推移領域の最も高い応力が上降伏点です。
D：下降伏点
下降伏点は、上降伏点の逆です。
E：破壊点
降伏点を過ぎると、応力とひずみは増加し続けます。
ある点まで到達すると、いよいよ応力は限界を迎えます。
これが破断点です。
上の応力ひずみ線図は実際には正しくありません。
応力の定義が外力に対して変形前の断面積で割っているからです。
応力を加えていくうちにひずみが起きつつ、断面積は下がる方向になります。
実際の断面積で割ると、線図は違ったものになります。
F：破断点
破断点を越えていくと、最後は割れます。
これが破断点です。
梁のたわみ
梁のたわみは材料力学の計算問題でよく出ますよね。
梁のたわみは微分方程式をゴリゴリ使う世界です。
力の作用条件や境界条件によって最終的な計算式が変わります。
実務上は書籍やネットなどで確認するとして、物理的に大事なことは
$$ δ∝\frac{FL}{EI} $$
という関係式が大事。
ここで\(F\)は力、\(L\)は梁の長さ、\(E\)はヤング率、\(I\)は断面2次モーメントです。
$$ I∝L^4 $$
という関係式も地味に大事。
\(F\)はターゲットとする力そのもので、\(L\)・\(E\)・\(I\)は材料の種類や形で決まる設計値です。
たわみ\(δ\)を特定の値以下に抑えることを目的とするのが、梁のたわみ計算。
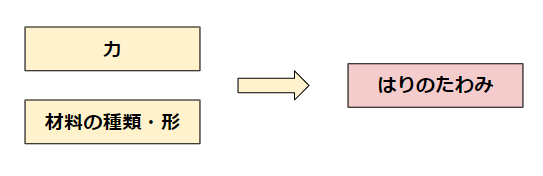
こんな関係式の中で議論するのが梁のたわみです。
土建設計や架台などの強度設計に使うので、アングル・チャンネル・H鋼などの部材選定に使います。
梁のたわみの式は、フックの法則を連続体に応用して多少の近似をしたら得られる法則です。
フックの法則が基本ですね！
薄肉円筒
薄肉円筒の強度計算は材料力学の範囲です。
これはタンクの強度計算に使います。
詳細はJIS B 圧力容器の構造に従いますが、原則は材料力学の問題です。
長手方向
$$ π{σ_z}Dt = \frac{π}{4}PD^2 $$
$$ {σ_z} = \frac{1}{4}\frac{PD}{t} $$
円周方向
$$ {σ_Θ}2t = PD $$
$$ {σ_Θ} = \frac{1}{2}\frac{PD}{t} $$
結論として長手方向の応力の方が円周方向よりも弱い1/2の関係にあります。
これは資格試験などでも出てくる有名な話。
フックの法則すら使わない簡単な数学の話から導出できます。
上側の式がモデルとして最初に導出する式で、下側の式が結果です。
厚肉円筒なのか薄肉円筒なのという境は化学プラントの圧力容器レベルでは考慮する必要はありません。
薄肉円筒一択です。
化学プラントでの使用例
応力ひずみ関係は材料力学で登場します。
これが化学プラントではどういう場面で使うでしょうか。
様々な分野で使います。
材料力学は構造設計のほぼ全てに登場します。
建築物の強度計算にフル活用します。
建築士の必須スキルの1つ。
装置の圧力容器の強度計算も応力ひずみ関係を使います。
ひずみゲージも応力ひずみ関係を使います。
静電容量式の圧力伝送器などがこの例です。
参考
最後に
化学プラントで使う範囲で材料力学について紹介しました。
材料力学上の用語・応力ひずみ・梁のたわみ・薄肉円筒の強度計算を紹介しました。
化学プラントでは土建設計・圧力容器の強度計算・ロードセルなどに使います。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）
*いただいたコメント全て拝見し、真剣に回答させていただきます。