化学プラントで使用される撹拌槽は、反応温度を安定させるために伝熱設計が重要です。しかし、伝熱計算は式が複雑で、運転条件によって変化するため、初心者にとってはハードルが高く感じられることもあります。
この記事では、撹拌槽の基本的な伝熱モデルから、境膜伝熱係数の考え方、蒸気ジャケットや内コイルの使用まで、現場で役立つポイントをわかりやすく解説します。トラブルがあった時や運転の検証をする時にも、考え方としては使えます。
この記事は、熱計算シリーズの一部です。
伝熱計算をここまで理解できれば化学プラントで大活躍
熱交換器の伝面計算だけを変えるときの考え方
熱交換器の伝熱面積だけを変えるときの計算方法
熱交換器の「汚れ係数」とは？設計で押さえたい基本と考え方
プレート式熱交換器の熱容量計算とは？Q=mcΔTの基本と設計ポイントを解説
撹拌槽ジャケット下鏡の伝熱計算の考え方
伝熱計算の例｜化学プラント槽型反応器
エアコンの冷却能力設計で大事な伝熱計算のイメージ
撹拌槽の伝熱モデル
撹拌槽の伝熱のモデルを最初に考えます。
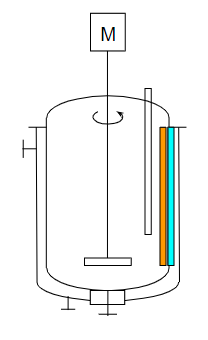
撹拌槽本体内部に撹拌機があり、外部にジャケットが付いている構造です。本体内部にプロセス液がありジャケットには冷却液を通すことで、プロセス液を冷却する場合を考えます。危険な化学反応を制御しようという場合によく見られる例です。この場合の胴板近辺を少し詳細に見ましょう。
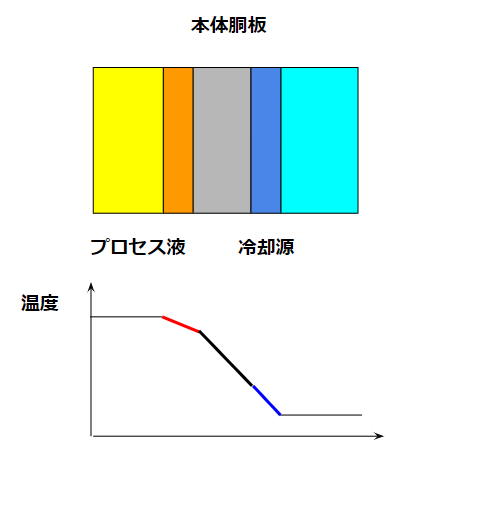
この図は伝熱工学としての伝熱計算でよく出てくる図です。胴板の直近のプロセス液と冷却液は厚み方向に温度分布を持ちます。この部分を境膜と呼びます。
境膜の外側は均一の温度で、胴板では温度分布があるけども、境膜でもある程度の温度分布を持つという考えです。この境膜部分の伝熱を計算するのは実は面倒です。
それが今回の伝熱計算のテーマ。今回紹介する伝熱計算をすることでU値を求めることが、一応は可能です。とはいえU値の計算は、運転条件の代表値を示しているだけであり、実際のU値と合っているか同課の検証は結構難しいです。
本体の境膜伝熱係数
本体側の境膜伝熱係数は一般に以下の式を使います。
$$ \frac{h_iD_T}{k}=C_1Re^aPr^b(\frac{μ}{μ_w})^c $$
文字はそれぞれ以下の意味です。
hi 境膜伝熱係数
DT 槽内径
k 内容液熱伝導度
C1 係数
Re レイノルズ数
Pr プランドル数
μ 液粘度
μw 壁面での液粘度
液粘度μとμwは温度が変わることで粘度が変わるという意味で、厳密には違う値となりますが、面倒ですので同じものとして考えます。
$$ \frac{h_iD_T}{k}=C_1Re^aPr^b $$
C1,a,bは撹拌機の形状によって決まる定数です。化工便覧などの専門書に記載があります。
ここまで整理すると、無次元数の比較をしているだけの式であることが見えてくるでしょう。求める値はhi(境膜伝熱係数)です。撹拌槽という機械の設計として設定可能なパラメータはDT(槽内径)とRe(レイノルズ数)です。レイノルズ数Reはその計算式中に撹拌翼の径がパラメータとして入っています。
プロセス液が決まることで他のパラメータはほぼ決まります。プロセス液として何を選ぶかということと、どの温度で運転するかということでほとんど決まります。
運転段階で調整可能な主なパラメータは回転数であり、レイノルズ数Reに影響を強く与えます。これは設計段階でも運転段階でも意識しておきたい大事なことです。
- 機械 槽内径・撹拌翼径
- プロセス 液の密度・粘度・熱伝導度（プロセス液と温度）
- 運転 回転数
ジャケットの境膜伝熱係数
ジャケットの境膜伝熱係数の式も、本体と同じように見てみましょう。
$$ \frac{h_oD_e}{k}=\frac{f(Re,Pr)}{g(Re,Pr)} $$
こういう式になります。右辺側がレイノルズ数Reとプランドル数Prで決まるといううことは同じです。Deはジャケット内流路の相当径と呼ばれるものです。
本体側の境膜伝熱係数では槽内径であったものを、ジャケット側の境膜伝熱係数では少し計算式が変わります。レイノルズ数Reも本体側とジャケット側では多少計算式が違います。共通しているのは式の構成。機械・プロセス・運転それぞれで決めることができる要素は変わりがありません。
右辺の式は以下の要素によって変わります。
- ジャケットに吹出ノズルが付いているか
- ジャケット内部に螺旋型のバッフルを付けているか
単純にジャケットを付けただけよりは、吹出ノズルやバッフルを付けることで、ジャケット内部の流れパターンが変わり、境膜伝熱係数が改善されます。
ジャケットに蒸気を使う場合
ジャケットに蒸気を使う場合は、計算式が変わります。蒸気を使って本体内部を温めるとき、蒸気は凝縮してドレンになります。この場合は、レイノルズ数Reの代わりに凝縮負荷Τという要素を考えます。
$$ Τ=\frac{W}{πD_j} $$
Wは蒸気流量、Djはジャケット内径です。
レイノルズ数に冷却液の速度の要素が入っていましたが、凝縮の場合は凝縮負荷の中に蒸気流量という要素として加わります。Τは蒸気流量をジャケット断面積で割った、ジャケット内部での蒸気平均流速を表すことになります。
コイルがある場合
槽内部にコイルがある場合は、計算式が1つ増えます。槽内部に入れるコイルなので内コイルと呼びます。これまで胴板を通じてジャケットだけから熱のやり取りを考えていましたが、コイルがあるとコイルからの熱のやり取りを考えることになります。
内コイルに関する設計要素としてはコイル径・コイル巻き径・コイルピッチがあります。コイル内部の境膜伝熱係数とコイル外部の境膜伝熱係数を計算することになりますが、計算式はかなり複雑になります。
大事なことは、コイルでの熱やり取りはとても大きいということ。計算式を眺める以上に、イメージで理解する方が良いと思います。
コイル外部の境膜伝熱係数は本体内部の境膜伝熱係数にほぼ近い（同じプロセス液で設置場所が壁面近くであるから）
コイル内部の境膜伝熱係数はジャケット側の境膜伝熱係数よりはるかに大きい（断面積が圧倒的に小さく、流速が高いから）
個人的には内コイルは賛成しません。メンテナンスが大変だからです。反応熱がとても高い危険な場合に限定した方が良いでしょう。
内コイル付きの撹拌槽を新たな反応向けに設置する場合はしっかり検討する必要がありますが、そうではない単純更新に近い場合は、細かな計算はしない方が良いでしょう。
時間が掛かるだけで得られる成果があまり高くはありません。
参考
伝熱計算は詳細の知識はなくても、概要は知っておきたいです。汎用的な教科書なら差はなく使えるでしょう。
関連記事
最後に
撹拌槽の伝熱設計では、胴板周辺の境膜伝熱係数を理解することが基本です。本体・ジャケット・内コイルのそれぞれで異なる計算式を使用しますが、原理を押さえておけば、運転条件や設置形態に応じて柔軟に対応可能です。伝熱計算は概略でも現場での検証やトラブル対応に十分役立ちます。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）
*いただいたコメント全て拝見し、真剣に回答させていただきます。
コメント