化学プラント建設のプロジェクトで、よく使う0.6乗則について分かりやすく解説します。

設備のコストって、ざっくりでいいから見積もれない?
こんなことを言われた経験は1度や2度ではないはずです。そんな時は、0.6乗則の出番です。
ラング係数とセットで、設備投資の概算見積で大活躍します。この内容を知っていると、社内の見積を超高速化することが可能。急遽見積をしてほしい!という製造課からの依頼に対しても、即日回答をして信頼感が一気に上がることになるでしょう。
社内で有利に仕事をできるようになりますよ。
この記事は、ラング係数シリーズの一部です。
ラング係数って何?化学プラントの投資概算見積
配管見積の考え方|初心者もわかる現場で役立つポイントと注意点
単価がプラント設備投資見積で大事になる理由
プロジェクト予算における労務費の考え方:オーナーズエンジニア視点から
この記事は、FSシリーズの一部です。
FS(フィージビリティスタディ)における余裕率の理解:ラング係数や設計係数が示す現実的なコストバッファ
化学工場のFSとは?基本と進め方をわかりやすく解説
知らないプラントの見積もりで不確実性を減らす方法|初心者向け解説
初期FSで差がつく!化学プラント設備投資に必要な“3つの確認事項”とは?
配管長さを超ざっくり数えるときのコツ|設備投資・設計・比較に役立つ思考法
配管見積の考え方|初心者もわかる現場で役立つポイントと注意点
0.6乗則とは
0.6乗則は、設備投資額がプラント能力の0.6乗に比例するという法則です。これだけ見ても分からないですよね。
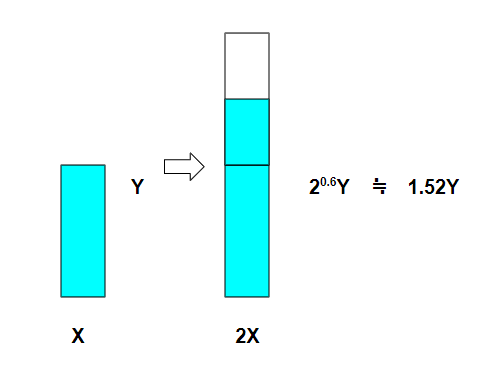
プラント能力Xの設備投資額がYであったとき、プラント能力2Xの設備の投資は単純比例の2Yではなくて、2の0.6乗(≒1.52)に比例した1.52Yとなるという法則です。
一般化すると、
$$ Y_2 = (\frac{X_2}{X_1})^{0.6}Y_1 $$
となります。
これは化学プラント建設の経験則で、膨大なデータを集めてわかった法則のようです。特に連続プラントでよく使われます。
というのも連続プラントはある製品を作るのに製法がほぼ決まっていて、プラントの構成もほぼ決まってしまうから。世界中どこでも似たような構成になってしまうようです。
バッチプラントなら一見すると、そうはいきません。作る製品がバラバラでそもそも同じ製品を作る工場の数が少なかったりします。でも、そんな細かいことは置いておいて、ざっくりした見積をしたいというときには、バッチプラントでも0.6乗則を使います。
どちらかというと、これしか方法がないから仕方ない的な思い切った発想ですけど・・・。

明日までに概算見積をしてほしい!

え・・・時間ないし・・・そうだ!0.6乗則でエイやっと出しておこう。怒られないだろう
こんな感じで見積をするときに使います。0.6乗則は文字通り0.6乗ですが、ケースによっては多少数値をいじることがあるようです。0.6~0.8くらいで値を振っている会社もあるのではないでしょうか。
プラント建設への適用例
バッチプラント建設時に0.6乗則を使うケースを考えましょう。連続プラントのように生産能力ベースでの議論は基本的にはできません。プラント内にどんな設備を置くかで投資額が決まる世界です。
この場合、ラング係数が活躍します。
| 設備 | ラング係数 | 単価 | 数量 | 小計(万円) | |
| 反応器A | 2,000 | 5 | 10,000 | 20 | 200,000 |
| 反応器B | X | 5 | 5X | 1 | 5X |
| ポンプ | 100 | 5 | 500 | 30 | 15,000 |
| 熱交換器 | 500 | 5 | 2,500 | 40 | 100,000 |
| 固有設備 | 10,000 | 5 | 50,000 | 1 | 50,000 |
| 合計 | – | – | – | 92 | 365,000+5X |
プラント建設をする場合は、設備一式を購入することになるのでラング係数が使いやすいです。
プラントサイズが反応器の数でほぼ決まるので、設備を基準にしてラング係数を当てはめます。
反応器Aが例えば10m3で2,000万円と分かっていた場合は、ラング係数をそのまま当てはめましょう。
ラング係数を5としたなら、
5×2,000=10,000万円(1億円)
と結果が出てきます。
未知の設備に対する補完
反応器Bは20m3だけど費用が分からない!という場合に0.6乗則の出番です。計算式をそのまま当てはめましょう。
(20/10)0.6×2,000=1.52×2,000=3,140万円
これにラング係数をかけて
5×3,140=15,700万円
となります。全体をまとめると以下の通りです。
| 設備 | ラング係数 | 単価 | 数量 | 小計(万円) | |
| 反応器A | 2,000 | 5 | 10,000 | 20 | 200,000 |
| 反応器B | 3,140 | 5 | 15,700 | 1 | 15,700 |
| ポンプ | 100 | 5 | 500 | 30 | 15,000 |
| 熱交換器 | 500 | 5 | 2,500 | 40 | 100,000 |
| 固有設備 | 10,000 | 5 | 50,000 | 1 | 50,000 |
| 合計 | – | – | – | 92 | 380,700 |
- 設備の大半の金額が分かっているけど、数個の特殊な設備の額が分かっていない
- 詳細の見積をメーカーに依頼するほどではない
という場合に0.6乗則で補完するという使い方をします。
全体に0.6乗を適用?
ここで、生産能力が反応器の数に比例すると考えて0.6乗を使うと考える人もいるでしょう。
今回の例では反応器20基に対して365,000万円なので、反応器Bを追加した21基のケースでは、
(21/20)0.6×365,000=1.03×365,000=375,950万円
となります。
| 数量 | 小計(万円) | |
| 反応器A系列 | 20 | 365,000 |
| 反応器B | 1 | X |
| 合計 | 21 | 375,950 |
このオーダーでは結果的には大差ありません。
固有設備は外だしして考えるべきだから、反応器20基に対して315,000万円で、21基の場合は
21/20)0.6×315,000=1.03×315,000=324,450万円
これに外だしの固有設備50,000万円を足して
324,450+50,000=374,450万円
| 数量 | 小計(万円) | |
| 反応器A系列 | 20 | 315,000 |
| 反応器B | 1 | X |
| 固有設備 | 1 | 50,000 |
| 合計 | 22 | 374,450 |
結果は大差ありません。
何となく数字遊びをしている感覚になります。
基準となる投資額が良く分からないのがバッチプラントの特徴なので、そこに0.6乗則を当てはめると雑な見積になってしまうと私は考えます。
0.6乗則は類似プラントのデータを集約させたものという前提がありましたよね。
バッチプラントで集約できるほどのデータがあれば良いのですが、そうではありません。
個別の設備にラング係数を当てはめる方が無難でしょう。
設備更新への適用例
バッチプラントレベルでは細かな設備投資レベルで0.6乗則が飛び交います。
プラント内の単一の設備改造や設備更新をする場合です。
考え方はプラント全体建設の場合と同じです。
個々の設備に対してラング係数を当てはめます。
例えば反応器Aの10m3が設置されている場所に、20m3の反応器Bを設置する場合の費用を見積もる場合、
(20/10)0.6×2,000=1.52×2,000=3,140万円
5×3,140=15,700万円
という計算結果になることは紹介しました。
個別の設備更新に0.6乗則を使う場合は疑ってかかりましょう。
世間一般で言われている法則通り計算したから絶対に正しい、という訳ではありませんので・・・。
全体に対する影響が少ない範囲で0.6乗を適用するなら目立ちませんが、単一の設備に対して0.6乗を当てはめようとすると誤差が目立ってきます。
設備本体額
10m3と20m3の価格差として0.6乗則を適用するかどうかという判断をしないといけませんが、基本的には問題ありません。
材料費の高騰や労務費の高騰など単価アップの要因がない範囲では概ね合います。
設備メーカーも同じ発想で考えるからです。
ただし製缶会社は割と水物なので注意してください。
ステンレスは割と高騰しやすい材質なので、0.6乗則では効かないくらい高騰するという場合もあります。
工事費
ラング係数を固定化する場合、工事費も0.6乗則が適用されることを前提としています。
これは実は相当怪しいです。
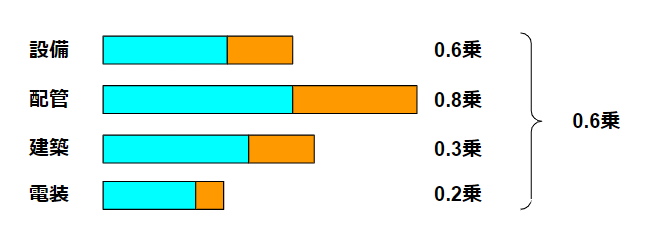
このように、配管工事と建築工事や電装工事は係数のかけ方が変わってきます。
0.6乗則とはこの辺を何となくまとめたときのことを想定しています。
例えば反応器1個を更新するレベルだと、
- 干渉物の脱着がどれくらいあるのか
- 基礎や梁を更新する必要があるのか(建築工事が発生するのか)
- モーターがサイズアップするのか
- 計器が追加したりするのか
という細かいレベルでかなり変わってきます。
ラング係数をこんな細かいレベルで適用すべきかという話にもつながります。
もちろんこんな細かい調査をする時間がないからこそ0.6乗則を使うわけですが、いざ0.6乗則を使ったときに数値が異常に高い場合には、この辺りを疑ってみて必要に応じて修正していく感じが良いと思います。
設備本体が0.6乗で効くのかどうかも疑わしく工事も0.6乗で効くか疑わしいので、まとめて0.6乗で出して金額が高くなっても止む無しというのが、最近の傾向だと思います。0.6乗則の数値が見た目で高いからと言って細かく数字をいじって下げたとしても、資材や労務費の高騰を吸収できずに予算オーバーとなる結果が増えています。どちらにしても予算オーバーするなら、0.6乗則で行ったというのが言い訳として使えるでしょう。結果的に0.6乗則に依存するとしても、数値を下げる可能性や費用の要素分割などの思考は持っておいた方が良いという例として紹介しています。
参考
設備投資は企業の戦略性が問われる重要な要素です。
公開されている情報はあまり多くはありませんが、以下のような書籍を見てみるのも1つの手でしょう。
関連記事
ラング係数や設備投資などを詳しく知りたい方は、以下の記事をご覧ください。
最後に
バッチ系化学プラントの設備投資に0.6乗則を適用させる例を紹介しました。
実際の設備コストは個別に見積もるのですが、0.6条則は「方向感」を掴むのにとても便利です。こういった設計のコツや考え方を、他の記事でも紹介していますので、ぜひ読んでみてください。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。(コメント欄はこの記事の最下部です。)
*いただいたコメント全て拝見し、真剣に回答させていただきます。
この記事の内容を、あなたの職場・キャリアに合わせて整理したい方に技術・キャリア相談を行っています。海外プラント、製造管理、組織の病理、キャリア停滞など、あなたの状況に合わせて具体的にアドバイスします
→ 技術・キャリア相談はこちら


コメント
you have a great blog here! would you like to make some invite posts on my blog?
pls, thank you