振動(vibration)について解説していきます。
多自由度系の典型例として梁の振動を取り上げます。
多自由度系とは二自由度を越える自由度を持つと考えて良いでしょう。三自由度くらいまでは解析をすることもあるでしょうが・・・。
梁の振動以外にも、板とかいろいろなパターンが存在しますが、梁が基本。
複雑な検討をするときにも、ちょっとくらいの誤解を恐れずに梁で検討することは多いです。
大学に入って材料力学で初めて登場する梁の概念ですが、大学院クラスでは振動の世界で応用的に登場してきます。
教科書的には式の導出を細かく見ていきますが、細かな計算はかなり省略して結果の解釈を中心に行います。
材料力学の知識をかなり使用していますので、細かい導出が気になる方は材料力学の学習を先に進めてください。私は当たり前のようにこの式を使っていましたが、逆に細かい導出はかなり忘れています。最初は、一自由度の振動系と対応が取れているということが分かれば、十分だと思います。
梁の振動(vibration)モデル
梁の振動モデルを考えましょう。
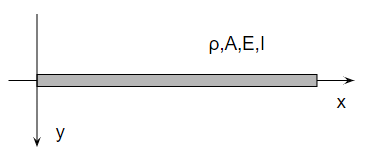
梁の世界になると、専門的になってきます。
定数の意味
- \(ρ\)：密度(kg/m3)
- \(A\)：断面積(m2)
- \(E\)：ヤング率(N/mm2)
- \(I\)：断面二次モーメント(mm4)
密度と断面積はそのままです。
ヤング率と断面二次モーメントは材料力学で登場する概念です。
どの定数も設計要素となりえます。
ただし、密度とヤング率は設計者の意図で変えることは難しく、断面積と断面二次モーメントを変えるというだけに留まるでしょう。
- 密度とヤング率 ： 材質を決めると自然と決まる
- 断面積と断面二次モーメント ： 物体の形状を決めないと決まらない
たわみ・たわみ角・モーメントの関係
材料力学ではたわみ、たわみ角、モーメントなどの概念があります。
| たわみ | たわみ角 | モーメント | せん断力 |
| \(y\) | \(Θ\) | \(M\) | \(N\) |
梁の長手方向を\(x\)・縦方向を\(y\)としたときの、\(y\)がたわみになります。
梁に力を加えて変形したときの変形量がたわみです。
たわみは\(x\)の値によって変わります。振動をターゲットにするので、時間¥(t¥)にも依存します。
これを意図的に表現するために以下の方式を使いましょう。
\(y(x,t)\)
\(f=f(x)\)で\(f\)が\(x\)に依存するという意味を表すのと同じです。
たわみ角、モーメント、せん断力はたわみと密接な関係があります。
- たわみ角\(Θ\)は、たわみ\(y\)を\(x\)方向に微分したもの。
- モーメント\(M\)は、たわみ角\(Θ\)を\(x\)方向に微分したもの。
- せん断力\(N\)は、モーメント\(M\)を\(x\)方向に微分したもの。
この辺の定義を基に運動方程式を作っていきましょう。
梁の運動方程式
梁の運動方程式と言えども、基本な同じです。
$$ ρA\frac{\partial^2 y(x,t) }{\partial t^2 }+EI\frac{\partial^4 y(x,t) }{\partial x^4 } = f(x,t) $$
この式はとても重要です。
これは
$$ m\ddot{x}+kx=f $$
という式と同じ形になります。
質量
左辺第一項は\(m=ρA\)という関係性を考えましょう。
これは梁の運動方程式が、以下のような梁の微小区間を考えているからです。
下のような微小区間\(dx\)の重さは\(ρAdx\)となります。
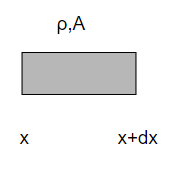
復元力
左辺第二項は復元力を示します。これは、やや難しいです。
梁を考える場合、微小区間\(dx\)にはせん断力\(N(x,t)\)が掛かると考えます。
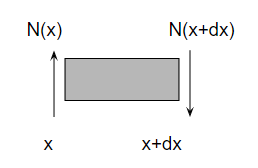
せん断力の方向は、材料力学の物をそのまま使っています。
この微小区間\(dx\)に掛かる力の合計は、
$$ \frac{\partial N}{\partial x}dx $$
と表現できます。
さて、モーメント\(M\)とせん断力\(N\)はそれぞれ以下のように表現できます。
$$ M = -EI\frac{\partial^2 y(x,t)}{\partial x^2} $$
$$ N = \frac{\partial M}{\partial x} $$
これらの関係を使うと
$$ -EI\frac{\partial^4 y(x,t)}{\partial x^4}dx $$
という力が微小区間\(dx\)に加わります。
外力
単位長さの梁に掛かる力を\(f(x,t)\)とすると、微小区間\(dx\)に加わる力は\(f(x,t)dx\)です。
単に掛け算しただけです。
左辺の２つの項と、右辺のいずれにも\(dx\)が含まれるので、削除すると運動方程式となります。
まとめ
梁の振動の運動方程式は、一自由度の振動の運動方程式と比較すると、以下の図のようになります。
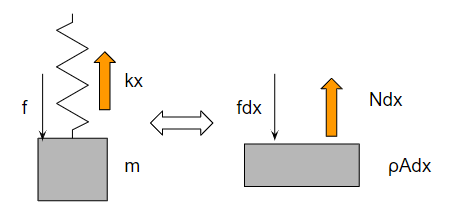
質量・復元力・外力から成り立っているという点で全く同じですね。
固有振動数
梁の運動方程式など複雑な計算を解くには、一般にはMATLABなどの数値計算ソフトに頼ります。
ここでは、固有振動数を求める方法だけを紹介しましょう。
フーリエ変換を使って、以下のように変数分離します。
$$ y(x,t)=φ(x)ψ(t) $$
位置に関する項と時間に関する項に分離した形です。
$$ ρAφ(x)\frac{\partial^2 ψ(t)}{\partial t^2 }+EIψ(t)\frac{\partial^4 φ(x) }{\partial x^4 } = 0 $$
$$ \frac{1}{ψ(t)}\frac{\partial^2 ψ(t)}{\partial t^2 } = -\frac{ρA}{EI}\frac{1}{φ(x)}\frac{\partial^4 φ(x) }{\partial x^4 } = C $$
時間に関する項
時間に関する項をもう少し見ていきましょう。
$$ \frac{1}{ψ(t)}\frac{\partial^2 ψ(t)}{\partial t^2 } = C $$
この解き方はかんたんです。
$$ ψ(t)=Ae^{iωt} $$
とフーリエ変換の形を取ります。
こうなると一自由度の振動系と同じ形になります。
\(t=0\)の初期条件で、位置や速度を定めると解けますね。（理論的には）
\(ω\)は固有振動数です。
位置に関する項
位置に関する項をもう少し見ていきましょう。
$$ -\frac{ρA}{EI}\frac{1}{φ(x)}\frac{\partial^4 φ(x) }{\partial x^4 } = C $$
これは以下の形で解くことが可能です。
$$ φ(x)=B_1sin(λx)+B_2cos(λx)+B_3sinh(λx)+B_4cosh(λx) $$
とりあえず、こんなものだと思ってください。
\(λ\)は固有モードと呼ばれます。
梁の場合は境界条件として末端部の条件が必要となります。
- 固定
- 自由
でたわみ・たわみ角などの条件を決めてしまいます。
境界条件さえ決まれば、\(ω\)と\(λ\)は1:1の関係で決まります。
固有モードについてはモード解析というもう少し専門的な話になりますので、今回は省略しましょう。
例えば片持ち梁の固有モードは下のような形をします。
特定の振動数の外力を受けて振動する梁は、これらの固有モードを重ね合わせた形でその振動数で運動します。
概念的にはフーリエ変換と似ていますね。
参考
化学プラントの機電系エンジニアで、振動に関して専門的な知識を持つ余裕のある人は少ないです。
もし勉強したいというのであれば、以下のような書籍が有用です。
関連記事
振動についてさらに知りたい方は、以下の記事をご覧ください。
最後に
梁の振動の運動方程式をエッセンス部分だけ抜き取って解説しました。
材料力学と振動工学の知識両方を必要とします。
解析的な解を求めるには限界があり計算ソフトに頼ることになりますが、その検証のためにはこのエッセンスの部分がとても大事になります。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）
*いただいたコメント全て拝見し、真剣に回答させていただきます。