振動工学(vibration)のちょっとした応用を、化学プラントに適用してみましょう。
振動問題は化学プラントでは起きにくいですが、起きたときには大問題。
ほぼ対処することができないからです。
設計段階でどれだけしっかりと設計するか、が全て。
基本的な考え方は振動工学の範囲内で解説できますので、本記事で紹介します。
設備設計のエンジニアとしては概要だけ知れば十分ですが、土建エンジニアはさらに専門的な知識を持っておきましょう。
思わぬ機械で、思わぬトラブルが起こったりします。振動は怖いですね。
梁や基礎に伝わる力のモデル
本記事では、動機器が振動したときに外部にどういう力が伝わるか、ということに着目します。
一自由度の振動のモデルを使いましょう。
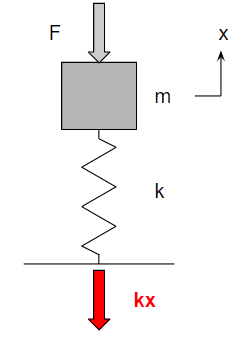
モデルは一自由度そのものです。
対象としている部分が、\(x\)ではなく\(kx\)というところがポイントです。
単に\(k\)を掛けただけでは解析としては足りません。
化学プラント的には動機器をちゃんと支持するための、梁や基礎などの土建的な場面で使います。
加振力
今回は動機器が周期的な運動をして、力が梁や基礎に加わる場面を想定しています。
角振動数\(ω\)で運転している設備は、ある重さ\(m\)による慣性力を発生します。
慣性力\(F\)を加振力として考えれば、シンプルな一自由度振動系をそのまま適用できます。
$$ F = mω^2 $$
\(m\)は設備の重さや内容液の重さそのものではありません。
\(m\)は動機器が運転しているときの重心のズレです。
動バランスという方が、設備エンジニア的には分かりやすいでしょう。
設備の重さや内容液の重さにも、もちろん依存します。
それだけでなく設備の形や内容液の運動の方法など、複雑に影響を受けます。
反応器の撹拌による液体の揺動も、もちろん対象となります。
梁・基礎に伝わる力
梁や基礎に伝わる力を評価しましょう。
$$ kx = X_0\frac{k}{1-(\frac{ω}{ω_0})^2} $$
周波数応答的には形はほぼ変わりありません。
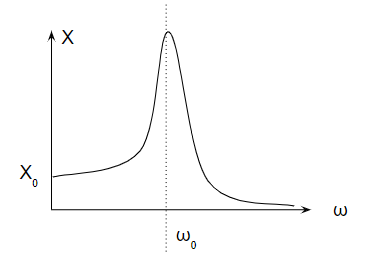
縦軸だけが変わります。（上の図は\(X\)のままですが・・・）
この式のまま眺めてみても良いのですが、固有振動数の形ではなく\(m,k\)の形に戻しておきましょう。
$$ kx = X_0\frac{k^2}{k-{mω}^2} $$
力を抑えるためには
上で導いた式の右辺を少なくすることが、土建設計上とても大事です。
土建設計上は、\(m,k\)の2つがパラメータとなります。
\(ω\)は運転条件によって変動するので、一般にはパラメータとなりません。
- \(m\)：大きくすると梁・基礎に伝わる力は下がる。
- \(k\)：小さくすると梁・基礎に伝わる力は下がる
\(m\)の設計
\(m\)を大きくすると、梁・基礎に伝わる力は下がると書きました。
これは\(mω^2\)が大きくなるからです。
この部分は固有振動数が下がると解釈する方が分かりやすいかもしれません。
\(m\)が大きくなると\(ω_0\)が大きくなるので、分母が無限に大きくなっていくと考えられます。
\(m\)を大きくするとは基礎の質量を上げるということ。
振動機器でバネなどの力で支持しないといけない機械には、機械に基礎をつけ足して重量を意図的に上げるという工夫をします。
化学プラントでは遠心分離機が良い例です。
\(k\)の設計
\(k\)はバネ定数のことで、バネを柔らかくすることで、梁・基礎に伝わる力は下がると書きました。
これは分子の\(k\)の項が大きくなるからですね。
単純に\(k=0\)なら、梁・基礎に力は伝わらないから当たり前の結果ですね。
ただし、設備は無限に振動するので壊れることは容易に想像がつくでしょう。
ここは設備メーカーが指定する値以上は確保しないといけませんね。
小型のポンプやブロアー程度なら、アンカーボルトなどで確実に固定しても、問題にはなりません。
逆にゴムなどを付けてしまうと、ポンプやブロアーが振動してしまって速度・加速度が高くなり設備を故障させることになります。
\(ω\)の考慮
\(k\)の設計と重なりますが、\(ω\)の配慮も知識としては知っていた方が良いでしょう。
運転の角速度である\(ω\)は、一般には固有振動数\(ω_0\)よりはるかに高いです。
振動機器を起動させて、回転数をどんどん上げていくと途中までは設備が大きく揺れて、そこからどんどん揺れが収まっていくシーンを見たことがあると分かりやすいと思います。
この設備が揺れているのは、角速度と固有振動数が等しくなる共振状態で振幅\(x\)が最大となる場所です。
この状態を継続していると、設備が故障します。
とても危険なので、設備の速度を上げるときには固有振動数近辺はすぐに通過するようにしましょう。
それでも何回も起動停止をしていると、設備はダメージを受けます。
だからこそTBMによる設備保全が大事ということですね。
この辺り、振動に関する知識がない設備保全者なら以下のような理解をしているでしょう。
- 運転をしていたらベアリングがダメージを受けて故障する
- 回転数が速い方がベアリングがダメージを受ける頻度が高い
これは正しいのですが、固有振動数や起動停止という概念を知っていれば、故障しやすい機器かどうかの優劣を付けるときの参考になると思います。
あくまで実績が正しいとすべきですが、その仕分や技術的な肉付けをする場合に役に立つと思います。
参考
関連記事
さらに知りたい方は、以下の記事をご覧ください。
最後に
動機器が振動することで梁や基礎に伝わる力の解析を行いました。
基本は一自由度の振動系です。
質量を上げることで対策とするのが一般的です。
バネ定数や角速度の上昇速度など設備設計や保全に関係する部分もありますので、知っていると一歩上のエンジニアとなりそうですね。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）
*いただいたコメント全て拝見し、真剣に回答させていただきます。
コメント