化学プラントの機電系エンジニアなら、最低限の知識として高校化学を理解しておく必要があります。
大学で化学を学んでいなくて忘れた機械系出身の人でも、危険物乙4の資格を勉強することで復習ができます。、
これを知っているかどうかは、プラントの設計はもちろん、保全や運転でも大きく違います。
知識としてだけでなく使いこなせるレベルになると、技術力として周囲から認められるようになるでしょう。
必要な範囲に絞って解説しましょう。
危険物乙4における物質の三態と化学プラント
危険物乙4（危険物第四類）で最初に学ぶことが物理的な基礎知識です。
そこで最初に出てくる項目が「物質の三態」
これは化学プラントの日常的な運転や設計と密接に関係しています。
物質の三態
物質の三態は、固体・液体・気体です。
「態」と「体」で間違えそうになりますよね。
固体・液体・気体の状「態」が3つあるから「三態」です。
物質を細かい目で見ていくと、分子・原子といったミクロな世界にたどり着きます。
これらをまとめて粒子と考えましょう。
粒子の状態
三態はこの粒子の状態が違います。
- 固体：粒子は強く引きあって規則正しく並ぶ
- 液体：粒子は緩く引きあってゆっくり動く
- 気体：粒子が自由に飛びあっている
固体・液体・気体のイメージを以下に示します。
実際に目で見えるわけでないから、イメージでしかありませんけどね＾＾
粒子間の引力
物質の三態は物質の運動と粒子間の引力の関係で決まります。
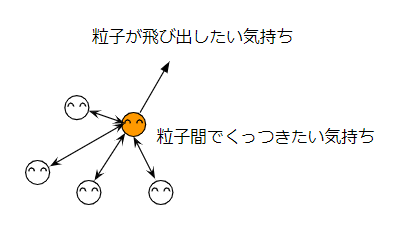
物質を構成する粒子は自由に運動しようという気持ちがあります。
一方、粒子間でくっつきたいという気持ちもあります。
この大小関係で、物質の三態が決まります。
- 固体：粒子間でくっつきたい気持ちが強い
- 液体：中間
- 気体：粒子が飛び出したい気持ちが強い
温度
物質の運動は温度が高いほど活発になります。
逆に、温度とは粒子の運動エネルギーの大きさとも言えます。
熱を加えるということは粒子の運動エネルギーを活発にするということ。
電子レンジなども同じ発想です。
以下はご参考まで。大学以降の知識が入っています。
数学的には以下のような数式で表現されます。
$$ T ∝ \frac{1}{2}\bar{m_i{v_i}^2} $$
\(m_i\)や\(v_i\)は粒子\(i\)を示します。
温度\(T\)が粒子の運動エネルギーの平均に比例するという意味ですね。
粒子間の引力
粒子間の引力は物質の粒子構造で決まります。
強く引力が働く物もあれば、弱いものもある。
粒子間の引力の大きさが融点や沸点に直結するため、融点や沸点が物質に固有な性質として決定されます。
下の雑な絵を見てください。
左のように粒子の形がシンプルだと結合はしやすいですが、右のような複雑な形だと結合はしにくそうに見えますね。
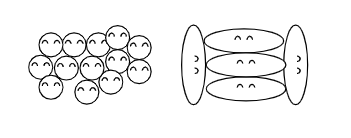
粒子の形は目に見えませんが、現実の眼に見える世界と同じと考えてよさそうです。
粒子の形が沸点に関係する
機械屋としてはこれくらいの知識で十分です。
固体
固体は化学プラントでは粉体という形で扱います。
ペレットのような規則正しい形のものもあれば、パウダーなどの粉塵が舞いやすいものまでさまざま。
原料や製品に粉体という固体の形で取り扱いをします。
危険物乙4の範囲では普通は固体としての扱いは少ないですが、化学プラントでは日常的に使います。
原料や製品が危険物第四類に該当するかどうかで、取り扱いが変わります。
特に輸送面でハードルが上がります。
輸送中に漏れて引火するリスクがあります。
液体の方がリスクは高いですが、固体でもリスクはあります。
固体だと例えば水でスプレーすることで、第四類を回避するという可能性も存在します。
リスクを少しでも下げるために、危険物第四類の固体としての扱いはできるだけしたくありません。
なお、危険物第五類だとハードルはさらに上がります。
液体
液体は化学プラントで日常的に使います。
原料としての有機溶媒・プラント内でのプロセス液・製造に伴って発生した廃油
いずれも液体の形で取り扱います。
理由は取り扱いが楽だから。
工場内ならポンプで自由にいろいろな場所に移送ができます。
外部とのやり取りもローリーなどで高い自由度で移送ができます。
固体だと配管での輸送が難しく、気体だと配管口径が高くなりすぎます。
液体であるメリットの大半は移送にあると言っても良いくらいです。
あとは化学反応にも有利というくらいでしょうか。
危険物乙4の取扱もほとんどが液体です。
液体を制すると危険物乙4を制し、ひいては化学プラントを制します。
物質の三態の中でも液体が最重要であることは、インプットしておきましょう。
気体
気体は化学プラントのプロセスで扱うのは、蒸留がメインでしょう。
化学反応で使用したプロセス液のうち、一部を取り出す作業として蒸留を行います。
この時に物質は気体の状態になります。
危険物乙4の範囲である有機溶媒も気体として取り扱いをします。
連続プラントでもバッチプラントでも日常的に関わります。
プラントの運転そのものよりも、プラントの保安防災の面で気体の取扱が大事になります。
これは危険物乙4でも重視されています。
高校の化学まででは触れていませんが、実務的には重要な内容。
融解凝固
危険物乙4で物質の三態を学んだ後に出てくるのが、変態。
変態とは三態の状態が変わることを言います。
融解と凝固
融解と凝固はそれぞれ以下の定義です。
- 融解：固体→液体
- 凝固：液体→固体
固体と液体という2つの状態に対して、どちらの状態に進むかということで融解と凝固を使い分けます。
これは中学理科の世界。
危険物乙4でも基本的にはこれだけの知識でOKです。
融解や凝固には以下の特徴もありますが、意識することはないでしょう。
- 融解熱と凝固熱が等しい
- 融解している時もしくは凝固している時は温度は変わらない
- 同一圧力での同じ物質の融点と凝固点は等しい
凍結
化学プラントでは水の凍結という現象が日常的に出てきます。
寒冷地でなくても冬場だと当然のように警戒します。
凍結が起こると液漏れが起こります。
これがなぜ起こるのか、ご存じでしょうか。
機械エンジニアなら説明できるようになっておきたいですね。
- 水が氷になると体積が膨張する
- 配管中で水で満たされていた部分が氷ると、体積が膨張しようとする
- 配管は体積が膨張しないように抵抗する
- 体積が膨張しない氷は高い圧力を抱える
- 配管が氷の圧力に負ける
- 強度の弱いガスケットが破壊する
- 昼になって温度が上がり、氷が水になると、ガスケットから水が漏れる
細かく書くとこのような現象になります。
この中で重要な事項は以下のとおり
- 水の比重が特殊
- 温度膨張
- 体積膨張
これだけでも1つの記事になるでしょう。
危険物乙4の範囲としては、水の比重が特殊ということだけは理解しておきましょう。
物質は普通、温度が低いほど体積が低いです。
凝固をすると体積が下がります。これは比重が上がることを意味します。
でも水だけは特殊。
水は氷になると体積が増え、比重が下がります。
氷水は氷の方が浮いていますよね。
水は4℃で比重が最も高くなるという特徴があります。
化学プラントに勤める機械屋としては、こんな特殊な例は水だけだと理解しておいて十分です。
ブライン
ブラインとは塩水と表現することもあるでしょう。
水の凝固点は普通0℃ですが、塩水は凝固点が0℃以下になります。
これを凝固点降下といいます。
小学校の理科の実験で取り組んだ記憶がありますね。
塩という異物があることで、水が氷になるのを邪魔するというイメージで結構。
塩の濃度が高い方が、凝固点降下は低いです。
化学プラントではこの原理を、冷却水として使用します。
塩化カルシウムや炭酸カリウムを混ぜた水をブラインとして使用します。
-10～-20℃程度まで冷やしたブラインを冷却源として使用します。
これは、そこまで低い温度で制御しないと危ない反応があるということです。
蒸発凝縮
危険物乙4で物質の三態を学んだ後に出てくるのが、変態。
変態とは三態の状態が変わることを言います。
蒸発と凝縮
蒸発と凝縮はそれぞれ以下の定義です。
- 蒸発：液体→気体
- 凝縮：気体→液体
液体と気体という2つの状態に対して、どちらの状態に進むかということで蒸発と凝縮を使い分けます。
これは中学理科の世界。
危険物乙4でも基本的にはこれだけの知識でOKです。
蒸発や凝縮にも、融解や凝固と同じように特徴があります。
- 蒸発熱と凝縮熱が等しい
- 蒸発している時もしくは凝縮している時は温度は変わらない
- 同一圧力での同じ物質の融点と凝固点は等しい
蒸発は日常生活でも例えば料理などで身近に利用しますが、危険性があります。
この危険性を理解するために乙4でも使っている表現がこちら
水が蒸気にあると体積は1700倍
これは一般知識として知っておいても良いです。
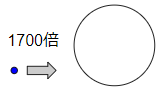
危険物の世界では、これを消火方法に利用します。
窒息効果を狙えるからです。
興味がある方は下記のサイトも参考にしてください。
蒸留
蒸発と凝縮は蒸留操作として化学プラントでは登場します。
- プロセス液の溶媒を回収する
- プロセス液そのものを留出する
- 大気に放出される溶媒を抑制する
バッチ系化学プラントではこれらの用途で使うことが多いです。
回収
溶媒には不純物もいっぱい含まれますが、このうちの純度が高い溶媒のみを取り出そうとしたときに、蒸留を使います。
蒸留ではまずは液を蒸発させます。
ここで不純物は蒸発せずに、溶媒のみが蒸発するような場合を考えます。
個々の物質に沸点を持っていて、沸点差を使用するのが蒸留。
不純物が沸点が高く溶媒が沸点が低いという状態です。
沸点の低い純粋な溶媒のみが蒸発していきます。
これを凝縮させて別の場所に移送すれば、蒸留の完成。
これを「溶媒の回収」という表現をします。
蒸留する物が溶媒で、蒸留をして回収するから、溶媒の回収です。
プロセス液を蒸留する場合は、プロセス液を回収するという言い方になります。
溶媒抑制
溶媒抑制はバッチ系化学プラントでの特徴です。
液をタンクに移送させたとき、タンク内の気相部は大気に逃げようとします。
液がタンクに入ってくるから、タンク内の気体は別の場所に行かないといけませんね。
ここで凝縮操作として溶媒抑制を使います。
大気に逃げる気相部には、溶媒が一部含まれます。
溶媒が気相部に含まれる量は、その気相部の温度に対する溶媒の蒸気圧で決まります。
温度が高いほど気相部に含まれる溶媒量が大きくなります。
ここで気相部を冷やすと、溶媒が凝縮して、大気に漏れる溶媒量が抑制されます。
水の性質
水の性質について紹介します。
- 融点は0℃
- 沸点は100℃
- 密度は4℃で最大で1000kg/m3
- 比熱は約4.2kJ/kg・K
- 蒸発熱は2256kJ/kg
- 蒸気になると体積が約1700倍
融点や沸点はセルシウス温度で表現しています。
セルシウス温度は日常的に使いますよね。
セルシウス温度の定義が水の融点と沸点そのものなので、融点0℃で沸点100℃というのは分かりやすいでしょう。
水の密度は4℃で最大となります。
他の物質では固体の方が密度が高くなりがちです。
比熱も水をベースにしています。
比熱4.18kJ/kg・Kと蒸発熱2256kJ/kgは化学プラントでも頻繁に使用します。
水と蒸気の体積は大気圧下で1700倍違います。
興味がある方は、下記のサイトも確認してください。
スチームによる加熱
水の性質で真っ先に使うのが、スチームによる加熱です。
化学プラントではプロセス反応のために温度を上昇させる場合、スチームを使います。
火をなぜ使わないかって？
周囲の危険物が燃えるからですよ。
高温のスチームを使って、プロセス液に加熱します。
スチームは圧力を数種類使いますが、100～170℃程度がバッチ系化学プラントの範囲。
実際にスチームを使って加熱する場合、下記のような計算をします。
トルエン(比熱1.679kJ/kg・K)の1000㎏を0℃から30℃まで上昇させるために、100℃まで10分で昇温させるために必要なスチーム流量は
トルエンに加えるべき熱量 = スチームの潜熱
という関係からスチーム流量を計算します。
トルエンに加えるべき熱量は次のとおり
1.679×1000×(30-0) = 50MJ
スチーム潜熱=スチーム凝縮熱量×スチーム流量だから
50×1000/2267×(60/10) = 132kg/h
となります。
スチームの凝縮潜熱を使ってスチーム流量を計算し、スチーム配管口径を算出します。
これは機械エンジニアでも日常的に行う計算。
冷却水による冷却
水は冷却水としても使用しますので、ここでも水の性質を使います。
とはいえこれは中学校理科の世界。
上のトルエンの例の逆を考えましょう。
トルエン(比熱1.679kJ/kg・K)の1000㎏を30℃から0℃まで10分で冷却させるために、必要な5℃の水の流量は
トルエンの冷却熱 = 水の比熱×水の温度差×水の流量
という関係から水の流量を求めます。
冷却熱は上の例と同じで50MJ
水の温度差は化学プラントでは一般に5℃で考えます。
これは冷凍機や冷水塔の設計条件に引っ張られます。
50×1000/4.2/5×(60/10) = 14280kg/h
の水が必要となります。
水の密度は1000kg/m3で考えますので、
14280kg/h = 14280m3/h = 238L/min
という結果になります。
この流量から水の配管口径を計算します。
水の比熱は4.2・密度は1.0と小数点1桁で切った概算値ですが、
計算結果である238L/minの1桁目にあまり意味はありません。
240L/minでも求めたい配管口径の結果は同じです。
精度が粗くていい場合はこういう概算値を使用します。
ポンプ・攪拌機の条件
ポンプや攪拌機の設計条件にも水の条件を使用します。
これは水の性質そのものを使うという話ではありません。
化学プラントのプロセス液は密度が1000kg/m3未満であることがほとんどです。
危険物第四類の有機溶媒を使うからです。
この条件でポンプや攪拌機のメーカーに設計させた場合、水運転時に運転できない可能性があります。
だからこそ水以下の比重の場合は水として計算することという文言を見積条件に加えることが普通です。
比重
危険物乙4でも特に大事な知識。それが比重です。いや、本当にめちゃくちゃ大事です。
比重というと中学校の理科などでも学ぶ範囲。
基礎的な知識だからこそ、実践的な分野である危険物取扱者でも大事です。
液の比重
液の比重の定義は以下のとおり、
物質の質量 ／ 物質と同じ体積・圧力の4℃の水の質量
温度・圧力は実際に意識することはほとんどないでしょう。
大気圧・4℃の水の1m3当たりの体積が1000kgなので、エンジニアとしてはこれだけを知っていてください。
比重の定義をもっと簡単に書くと、水の何倍重たいかこれだけです。
比重1.2なら、水の1.2倍の重たさで、現実的には1.2×1000=1200kg/m3の密度を持つことを意味します。
ガスの比重
ガスの比重の定義は以下のとおり、
蒸気の密度 ／ 空気の密度
空気の密度は0℃、大気圧下で1.2kg/m3程度です。
これも化学プラントの機械エンジニアなら微妙に使う数字です。
蒸気の密度が0.8なら、1.2×0.8=0.96kg/m3です。
ちなみに、気体の比重を考えるとき、分子量で考えた方が分かりやすいです。
蒸気の密度 ／ 空気の密度 ＝ 蒸気の分子量 ／ 空気の分子量
という関係があるからです。これは後で解説しましょう。
空気の分離用が28.8であることは知っておいた方が良いです。
これは空気の組成が窒素79%・酸素20％程度で、窒素の分子量28と酸素の分子量32を
加重平均した値です。
液体・気体の比重については、下記のサイトも参考になります。
動力計算・圧損計算・計器設計
化学プラントでは比重は動力計算や圧損計算に使います。
実際には比重ではなくて密度を使います。
動力計算では水より軽い物質つまり比重が1以下でも、水と同じだと考えて計算します。
圧損計算でも当然ながら密度を使います。
計器では密度が計算式そのものに直結します。
流量計や液面計が典型例です。
機電系エンジニアとしては密度は基本的なパラメータとして認識しておきたいですね。
分液
化学プラントで比重というと分液操作に使用します。
分液なので液の比重がテーマ。
分液とは水と油の混じり合わない液体を、物理的の除去する操作です。
バルブやポンプを使った操作です。
分液は時にすごくやりにくい場合があります。
水層と油層の間の中間層が判別できないという場合です。
これは水層と油層の密度が近い時つまり比重が近い時に、特に起こりやすいです。
分液性が比重差に直結します。
水層と油層の比重が近い時に、意図的に比重差をつけるために、水層に薬液を加える場合があります。
バッチ系化学プラントの場合、苛性ソーダをちょっと加えることが普通です。
分液操作に関連して危険物第4類の液はほとんどが比重1以下です。
これはぜひ習得しておくべきです。
水層が下層、油層が上層になります。
ガス検知器
ガス検知器は言葉どおり、ガスを検知する機械です。
家庭や事務所では煙感知器を天井に着けますね。
これと同じ感覚で、危険物が漏れたことを検知するための機械を付けます。
これはできるだけ低いところに置きます。
というのも危険物第四類のガスの比重は1以上がほとんどだから。
危険物第四類は液体の状態で比重1以下、気体の状態では比重1以上という面白い関係があります。
ガスは空気より重たいので、できるだけ低い位置に溜まろうとします。
煙は空気より軽いのは、温度が高いからですね。
分子量的には、危険物第四類の有機溶媒ガスも火災時の煙も、空気より高い分子量を持っています。
この辺はちょっと難しいですね。
気体の状態方程式
危険物乙4では圧力について直接取り扱うことがあまりありません。
気体の状態方程式も出番はそこまで多くはありません。
危険物乙4や化学プラントで使う気体の状態方程式の定義は、以下の定義でOKです。
$$PV=nRT$$
\(P\)が圧力、\(V\)が体積、\(n\)がモル数、\(R\)が気体定数、\(T\)は温度です。
気体の比重計算でも状態方程式は使用します。
ボイル・シャルルの法則
気体の状態方程式はボイル・シャルルの法則から派生しています。
ボイルの法則とシャルルの法則という2つの法則があります。
ボイルの法則が一定質量の体積の気体は、圧力に反比例し、温度に比例する
シャルルの法則が圧力が一定なら、気体の体積は温度に比例する
という関係です。
ボイルの法則が
$$\frac{P}{T}=const.$$
シャルルの法則が
$$\frac{V}{T}=const.$$
という関係ですね。
この辺は教科書にいっぱい記載していますので、省略しましょう。
例えば、以下のサイトが参考になります。
理想気体
先ほど提示した気体の状態方程式、
$$PV=nRT$$
これって使用できる範囲が限定されています。
圧力や温度が常温から外れていると誤差が生じます。
これは物理学のあらゆる分野で発生しますよね。
限定した場所において線形化して簡単な式で表現する。
大事なことです。
現に化学プラントのエンジニアリング程度だとこの式を使うだけで十分ですので＾＾
気体定数
気体の状態方程式には\(R\)という定数が出てきますよね。
$$PV=nRT$$
これは、こんなものだと思っていれば十分です。
1molの気体が0℃、0kPaGにおいて22.4Lであるという関係を\(R\)という定数にしているだけです。
これを多数の実験をして見つけ出したことが凄いのですが。
我々としては先人の知恵を使って、その先のことを考えるしかないでしょう。
モル数
気体の状態方程式は
$$PV=nRT$$
という形で見るときれいですが、ちょっと解釈が難しくありませんか。
私は
$$\frac{PV}{T}=nR$$
という方が解釈しやすいです。
ボイル・シャルルから派生していることも一目で分かり
\(P\)、\(V\)、\(T\)という我々が操作可能なパラメータが
\(n\)という物質の量そのものを決める。
解釈としては非常に分かりやすいと思いませんか。
・・・話が脱線していますね。
減圧蒸留
化学プラントで気体の状態方程式が登場するのは減圧蒸留でしょう。
バッチ系化学プラントの例で見てみましょう。
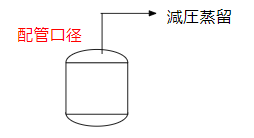
反応槽にあるプロセス液を減圧蒸留します。
ここでエンジニアとして考えるべきことは配管口径
これをミスすると運転できません。
- 配管口径が小さすぎると圧力損失が大きくなり、真空ポンプの能力が足りない
- 配管口径が大きすぎるとコストが掛かり過ぎる。
ここで最適な配管口径を選定するために、気体の状態方程式を使います。
減圧高温で体積は膨張
改めて、気体の状態方程式を見てください
$$PV=nRT$$
減圧蒸留というのはこの状態方程式上でどういう意味があるでしょうか？
減圧なので\(P\)が小さく、蒸留するので\(T\)が大きい。\(nR\)が同じなら、\(V\)が大きい。
こういう意味があります。
減圧蒸留の度合いが強いほど、体積は膨張していきます。
例を見てみましょう。
10kPaA、100℃の状態では、100kPaA、30℃で1m3の体積はどれくらいになっているでしょうか？
$$\frac{100}{10}\frac{100+273}{30+273}=12.3$$
なんと12.3倍！
凄いですね＾＾
減圧蒸留の設計ファクター
減圧蒸留の配管口径を決めるには、結構複雑な要素が絡みます。
- 反応で必要な真空度
- 真空ポンプ能力
- 配管圧力損失
- 加熱スチームの流量
- 凝縮コンデンサーの伝熱面積・冷却能力
これらのファクターを個々に計算して、ボトルネックが加熱スチーム流量となるように決めるのが普通です。
加熱スチームがボトルネックというのは、加熱スチーム量が足りないからこの状態でしか運転できないという状態。
スチーム量を上げれば運転能力はもっと上がるかもしれないが、設備の能力が足りなければ危険な状態に移ってしまいます。
ここの考え方は、化学プラントの機械エンジニアでもかなり深い部分です。
多くの設計ファクターのうちの配管の圧力損失を決めるために
気体の状態方程式を使う。
これだけを理解してもらえればOKです。
熱量の定義
危険物乙4では熱量を直接議論することは多くはありません。
でも危険物の取扱が燃焼に直結しているので、熱量は当然ながら関連します。
熱量は中学校の理科で学ぶ範囲ですよね。
比重などと同じく基本的な分野ほど大事ということです。
以下のサイトも参考になります。
温度
温度って日常生活で当たり前のように使っていますよね。
今日は10度だ、明日は30度だ、など。
この度は実は℃ですよね。
セルシウス（セ氏温度）といいます。
定義は簡単.
大気圧での水の融点を0℃、沸点を100℃として、100等分したもの
物理化学の世界では絶対温度という表現を使います。
絶対温度 ＝ セ氏温度 ＋ 273という関係があります。
単位は℃ではなくKです。
ボイルシャルルの法則などでも何気にこの関係式を使いますね。
熱量
熱量とは何でしょうか。
熱の量のことですね。
あらゆる物質はエネルギーを持っています。
エネルギーにもいろいろな種類があり、物理を学んだ人なら運動エネルギーや位置エネルギーなどを思い浮かべるでしょう。
運動エネルギーなら速度に関連したエネルギー、位置エネルギーなら高さに関連したエネルギー。
これらと同じで熱量は温度に関するエネルギーと考えればいいです。
大学で熱力学を学べばエンタルピーとか登場しますが
そんなものは化学プラントではほとんど使いません。ごくまれに使うかな？
熱量の単位はcalだったりJだったりします。
私はこの年になってもいつも関係性を調べてしまいます。
- 1J=0.24cal
- 1cal=4.2J
実際に上の値を記憶を頼りに入力したら、真逆に理解していました。
毎日使うわけではない関係式なので、覚えられませんね。
単位換算で計算結果が大きく変わってしまいますので、面倒でも丁寧に調べた方がいいですよ。
比熱
比熱は物質の温度を1℃上げるために必要な熱量というのが定義です。
温度を\(T\)、熱量を\(Q\)としたら、比熱\(C\)は質量\(m\)を使って
$$Q=mCT$$
と表現できます。
\(C\)の単位はJ/kg・Kですね。
どうでもいいですが、J/kg・Kだと
$$\frac{J}{kg}K$$
なのか
$$\frac{J}{kg・K}$$
なのか迷います。
特にExcelでの計算では間違えの元です。比熱の単位は後者ですよ。
比熱も大学の熱力学を学べば定積モル比熱や低圧モル比熱など出てきますが、
これも化学プラントでは全く意識しませんね＾＾
熱交換器の設計
熱量は熱交換器の設計で登場します。
ざっくりしていますか。
熱に関する計算のほぼ全てが熱交換器の設計で出てくるから仕方がないですね。
というのも熱交換器の設計の課題が〇kgの□を△℃から▲℃まで×時間で変化させるというモノばかりだからです。
熱交換器！何か知らないけど難しそう！
と思うかもしれませんが、設計課題は中学校の理科そのものです。
これを複雑にしていっただけ。
課題の最初のアプローチは熱量の計算から入ります。
1000kgのメタノールを30℃から60℃まで1時間で上げる
という熱交換器を設計する場合、最初に熱量を計算します。
メタノールの比熱がだいたい2.47kJ/kg・Kなので
1000*2.47*(60-30)/1=74,100kJ/h
という計算を最初にします。
ここで時間の単位が出てくるのが化学プラントっぽいです。
中学校の理科なら時間を考えませんよね。
この74,100kJ/hの熱交換をするためには、
- どれだけの伝熱面積が必要か
- どういった加熱源を準備すればいいか
- 材質や構造をどうすればいいか
というような具体的な装置の設計をしないといけません。
ここが機械エンジニアの考えるところです。
冷凍機・冷水塔
熱量の概念は冷凍機や冷水塔でも登場します。
これは熱交換器そのもの。
熱交換器の方が数も頻度も圧倒的に多いので外出ししていますが
冷凍機や冷水塔でも発想は同じです。
ポンプ
ポンプで熱量？
そう思った人はいませんか？
実は登場します。それが、締切時の温度上昇。
ポンプを締め切った状態で運転すると、ポンプに加える電力エネルギー ＝ ポンプの内容部の温度上昇に使われると考えて良いです。
電力エネルギーはJの単位ですよね。時間単位で考えるのでJ/h。
これって熱交換器の設計で出てきた熱量の考え方がそのまま使えます。
とはいえ、締切時の温度上昇を計算するシーンはありません。
そんな状態にたどり着かないように運転をするのが普通だからです。
単に関係性がありますという理解をしていれば良いと思います。
膨張
膨張って何でしょうか？
改めて考えるほどでもないくらい、日常生活でありふれています。
ここでは自然科学で使う膨張に限定します。
膨張は温度上昇を行うと必ず発生します。
線膨張と体膨張
膨張に関して線膨張・体膨張に分けて定義することもあります。
膨張の模式図は以下のとおり。
温度が増えると、増えた分だけ膨張します。
これを1次元だけを考えると線膨張、3次元まで考えると体膨張というだけです。
細長い配管のような形状だと、長さ方向だけを考えて議論することも多いので
線膨張で考えて良いでしょう。
物質の三態と線膨張・体膨張
線膨張で考えて良いか体膨張で感g苗て良いかは、物質の三態と関係があります。
| 三態 | 線膨張 | 体膨張 |
| 固体 | 〇 | 〇 |
| 液体 | 〇 | × |
| 気体 | 〇 | × |
【マニアック】線膨張と隊膨張
線膨張と隊膨張の関係を数式で確認してみます。
マニアックなので興味がある方だけご覧ください。
膨張前の長さを\(l_0\)、膨張後の長さを\(l_1\)、線膨張率を\(α\)、温度変化を\(Δ\)とすると、
$$l_1=l_0(1+αΔt)$$
線膨張だとこれだけでOKです。
隊膨張だと\(x,y,z\)方向を考えないといけません。
$$l_{x1}=l_{x0}(1+α_xΔt)$$
$$l_{y1}=l_{y0}(1+α_yΔt)$$
$$l_{z1}=l_{z0}(1+α_zΔt)$$
とそれぞれ添え字を付けて、3辺を全てかけると
$$l_{x1}l_{y1}l_{z1}=l_{x0}l_{y0}l_{z0}(1+α_xΔt)(1+α_yΔt)(1+α_zΔt)$$
となります。これは下のように簡略化して書くことができます。
$$V_1=V_0(1+βΔt)$$
この\(V_0\)や\(V_1\)は体積を示します。\(β\)が体積膨張率です。
細かい近似は抜きにして、とりあえずこう考えておけばOKです。
気体の体膨張率はボイルシャルルと近い
気体の体膨張率はどれくらいでしょうか？
ほとんど1/273です。
これってどこかで見たことがありませんか？
そうです。ボイルシャルルの法則です。
$$PV=nRT$$
ですが、\(T\)は絶対温度で表すと
$$PV=nR(T+273)$$
同じ圧力で、温度が1℃上がったときの体積変化は
$$ΔV=\frac{V_1}{V_2}=\frac{T_1+273}{T_2+273}=1+\frac{1}{T_2+273}$$
と表現されるので、1/273に近い値になります。
液封
膨張は液封の原理として登場します。
液封はボール弁で有名。
液封のメカニズムを紹介しましょう。
- 液体がある場所に閉じ込められていて、気体や固体のスペースがない。
- 閉じ込められた液体の温度が上昇する。
- 温度膨張を抑えるために必要な圧縮力が、周囲の強度を越えると破裂
「温簿上昇による膨張」と「体積の圧縮に必要な力」のバランス関係で決まります。
液体は一般に体積圧縮力が非常に大きいので、簡単に液封が起こります。
体積圧縮に必要な力が大きいとは、液体を圧縮させるために必要な力が大きいという意味です。
気体だと体積圧縮に必要な力が小さいので、こういう現象は起きません。
固体だとある場所に閉じ込められることはなく、気相部が必ず残ります。
ベアリングの取付
回転機の軸にベアリングをセットする場合、ベアリングを温めてから軸にセットします。
これはベアリングを膨張させて、軸にようやくはまる程度の寸法差にしています。
ベアリングが元の温度に戻ったときに、縮む力が働くので、
ベアリングが軸に強烈な力で固定されるというわけです。
化学プラントでは回転機によく使っていますよ。
気が付かないことが多いですけどね＾＾
エネルギー保存則
エネルギー保存則ってご存じですか？
高校で物理を学んだときに以下のような関係式に出会います。
$$ mgh + \frac{1}{2}mv^2 = const.$$
位置エネルギー＋運動エネルギーが不変という法則です。
これは古典物理学における剛体のエネルギー保存ですね。
エネルギーとしてどこまでを考えるか？という問題があります。
例えば、流体になると圧力エネルギーも考慮したベルヌーイの法則として有名です。
熱力学第一法則
危険物乙4ではエネルギー保存則として以下の関係を考えます。
$$ΔU = Q + W $$
これは熱力学第一法則と言われます。
物体に与えられた熱量と仕事が内部エネルギーの増加に使われる
こういう法則です。
内部エネルギー変化 ＝ 熱量変化 ＋ 仕事変化
とこの記事では呼ぶことにします。
気体のピストン運動をイメージして学習することが普通でしょう。
以下のサイトも参考になります。
火災爆発
エネルギー保存則では運動エネルギーや位置エネルギー、さらに圧力エネルギーなどを考えるのが普通そうですが、なぜ乙4ではそれらを考えないのでしょうか？
これは内部エネルギーの方が遥かに強大だからです。
危険物乙4では火災爆発を重要なテーマとして考えます。
火災爆発が起きた時、内部エネルギーの急激な変化を伴います。
ここでエネルギー保存則を考える場合、内部エネルギーの変化量が
運動エネルギーや位置エネルギーの変化に寄与する割合は非常に低いです。
熱力学第一法則どおり、熱量変化と仕事変化への寄与度が高いです。
そのため、運動エネルギーや位置エネルギーは無視して考えます。
熱力学第一法則の展開
先ほどの、熱力学第一法則
$$ΔU = Q + W $$
これは「変化」をテーマにしています。
この変化は現実世界には様々ありますが、熱力学では典型例を4つ考えています。
- 断熱変化(\(Q=0\))
- 等圧変化(\(ΔP=0\))
- 等積変化(\(ΔV=0\))
- 等温変化(\(ΔT=0\))
細かい式展開は無視しますが、単原子分子気体の場合は熱力学第一法則は以下のように書くことができます。
$$ΔC_vΔT= Q + PΔV + VΔP $$
爆発は断熱膨張
危険物乙4で興味がある火災爆発。
これは熱力学第一法則的には断熱膨張に分類されます。
断熱膨張とは、熱量の変化がないということ。
少しわかりにくいですね。
爆発を起こすということは物質の内部にあるエネルギーを外部に急拡散するということです。
ここで内部エネルギーが急激に下がります。
この変化が全て、仕事変化として使われます。
仕事って何でしょうか？
\(ΔPV\)で示される。気体の圧力と体積の変化です。
高圧の気体が大気圧まで急激に下がり、体積が急膨張します。
爆発を起こしたときはこの変化速度があまりにも早いので、熱をどこかに伝える時間がありません。この意味で\(Q=0\)です。
だからこそ、爆発は断熱膨張としてみなします。
先ほどの熱力学第一法則に沿って見てみましょう。
断熱変化(\(Q=0\))の場合は、熱力学第一法則は
$$ΔC_vΔT= PΔV + VΔP $$
と展開できます。
左辺が内部エネルギーの変化です。
火災爆発が起きると内部エネルギーは減少します。温度が下がると考えて良いでしょう。
この変化分が右辺の仕事変化に変わります。
仕事変化は理想状態ではもう少しきれいな表現が可能です。この辺は熱力学を学習する方が良いでしょう。
化学プラントではそんな学問よりも、爆発を絶対に起こさせないという意気込みの方が遥かに大事ですよ＾＾
その意味で今記事は、爆発に関する学術的な知識という意味で参考程度に見ていただければと思います。
参考
危険物乙4は試験としての意味もありますが、化学プラントの場合は実務に直結する重要な資格です。
内容は割と簡単ですが、一瞬だけ暗記してすぐに忘れて良い物ではなく、長く使っていくものです。
座右の銘として何か一冊は手元に置いておきましょう。
関連記事
さらに知りたい方は、以下の記事をご覧ください。
最後に
危険物乙四の範囲内で物理化学の基礎について解説しました。
物質の三態・蒸発・凝縮・水の性質・比重・状態方程式・熱量・膨張・エネルギー保存則
高校の化学で学ぶ範囲のことですが化学プラントでは絶大な効力を発揮します。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）
*いただいたコメント全て拝見し、真剣に回答させていただきます。
コメント