冷凍サイクルや空調設備の設計・運転管理で欠かせないのが、p-h線図(圧力‐エンタルピー線図)を用いた熱力学の理解です。p-h線図は冷媒の状態変化を視覚的に把握でき、凍結サイクルの解析や効率改善に役立ちます。
本記事では、凍結サイクルの基本とp-h線図の読み方を初心者にもわかりやすく解説します。
冷凍機の資格や熱力学の勉強で登場する分野です。オーナーエンジニア的にはメーカーに任せてしまえる部分なので、意識していないかもしれません。
知っておいた方がちょっと便利な知識、という位置づけかもしれませんね。この辺りの知識をしっかり使えるレベルにしていると、実はトラブル解析時に役に立ちます。
冷凍サイクルとp-h線図(p-h diagram)
冷凍サイクルを考えるときにp-h線図という謎の関係が登場します。
今回はこのp-h線図をちょっと深堀りします。
冷凍サイクルは以下のような、教科書的なものを考えましょう。
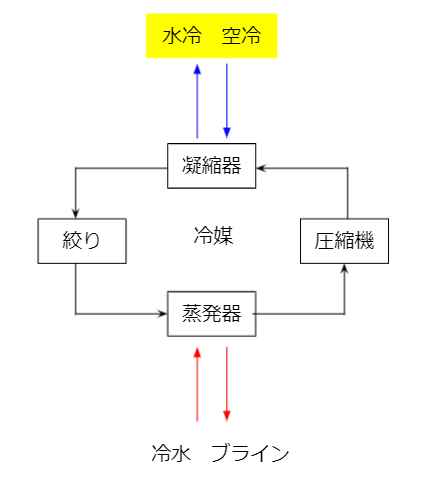
今回の主役は冷媒です。
冷媒は冷凍サイクル内をグルグル回ります。
回っている間に状態が変化します。
冷凍機のどこでどの状態になっているかは、冷凍機を知るうえでとても大事です。
状態を示す指標は熱力学的にはいろいろあります。
今回は圧力PとエンタルピーHを使います。
p-h線図は以下のような形をしています。
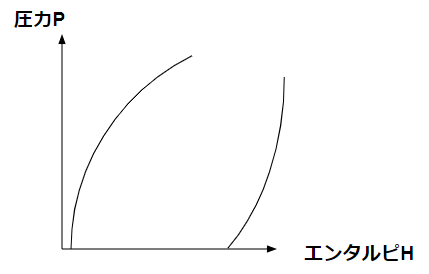
良く分かりませんよね。
大丈夫です。
ゆっくり見ていきましょう。
エンタルピー
そもそもエンタルピーとは何でしょうか?
エンタルピーHは内部エネルギーUと圧力P・体積Vを使って以下のように定義されます。
Hは内部エネルギーUと圧力P・体積Vを使って以下のように定義されます。
$$ H = U + PV $$
良く分かりませんよね。
大丈夫です。
内部エネルギー
内部エネルギーUとは分子の運動エネルギーと考えていいです。
物質は分子が非常に多く集まってできています。
この分子は目に見えないけど常に運動をしています。
このエネルギーは温度に比例します。むしろ温度の定義といってもいいくらいです。
温度は熱力学的には状態量と呼ぶことがあります。
これは物質の状態を指定するために必要な物理量のこと。
1つの状態量だけで物質の状態を決めることはできず、複数の状態量を組み合わせます。
日常生活で「20℃の水」「10℃の気温」なんて表現を使うときに、水や空気の状態を示すために温度という状態量を使っています。
流体エネルギー
PVは流体エネルギーという位置づけで良いでしょう。
圧力Pと体積Vの掛け算です。
こんなものか・・・程度でいいと思います。
考えると難しくなります。
流体の状態を指定するためには、圧力Pや体積Vが必要ということです。
圧力Pや体積Vも温度Tと同じで状態量です。
「20℃の水」「10℃の気温」なんて表現するときには「100kPaAの大気圧」を実は想定しています。
2つの状態量
温度と圧力が指定できれば、理想気体なら体積が決まります。
状態量の2つを指定すればほかの状態量が決まるという意味です。
エンタルピーHは温度Tに依存する内部エネルギーと圧力P・体積Vで決まる流体エネルギーを足し合わせたものです。
温度Tも圧力Pも体積Vも物質の状態量であるので、エンタルピーHも状態量です。
そこで圧力PとエンタルピーHという2つの状態量でみると都合がよかったのが、冷凍機だと認識すれば良いでしょう。
変化量
エンタルピーHは状態量ですが、その値そのものには実はあまり興味を持ちません。
変化量に興味を持ちます。
圧力Pや温度Tは絶対値に興味がありますよね。100kPaとか20℃というように。
ところが、エンタルピーHは絶対値に興味がありません。
変化量を知ろうとしたら、数学的には微分をすることになります。
$$ dH = dU + PdV + VdP $$
こんな関係式になります。
例えば固体だとdV≒0とみなせるくらい変化量が少なく、圧力変化を気にするようなシーンはほぼないので、dH = dUとみなすことが多いでしょう。
つまりエンタルピーと言いつつ、実質内部エネルギーを見ているという意味。
もちろん、圧力を過剰にかけたりする系ではVdPの項が影響してきます。
一方で、気体だとPdVもVdPも変化します。
実際の機械などでは体積一定もしくは圧力一定の条件で運転することが多いでしょう。
液体の場合は個体と同じくPdV≒0ですが、VdP≠0です。
| PdV | VdP | |
| 固体 | 0 | 0 |
| 液体 | 0 | 変化 |
| 気体 | 変化 | 変化 |
ざっくりこんな理解で良いでしょう。
態とp-h線図(p-h diagram)
p-h線図では冷媒の状態変化が分かるようになっています。
便利ですね。
さて、p-h線図上で冷媒はそれぞれどんな状態になっているでしょうか。
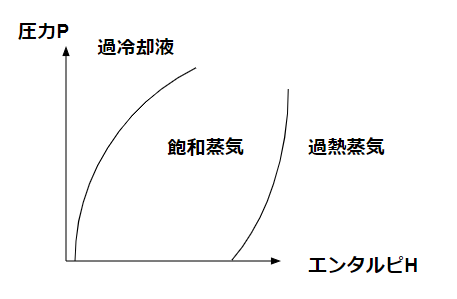
過冷却液・飽和蒸気・過熱蒸気という3つの区分があります。
過冷却液がいわゆる液体の部分、過熱蒸気が気体の部分です。
飽和蒸気は液体と気体が一定量混じっている状態ですね。
エンタルピーHが低い側が液体です。
これは液体の方が気体よりも温度が一般に低いこと(Uが低い)と、液体の方が気体よりも体積が小さいこと(PVのVが低い)からわかりやすいでしょう。
圧力一定
p-h線図上で簡単な状態変化の例を紹介しましょう。
まずは圧力一定の条件。
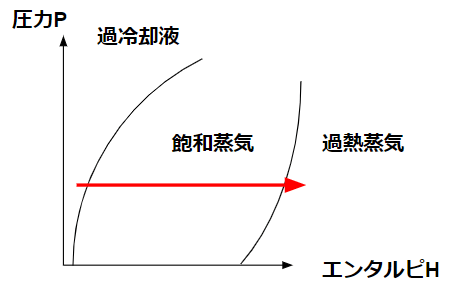
冷凍機では蒸発器や凝縮器での変化が圧力一定の条件になります。
圧力一定なので縦軸は一定です。当たり前です。
圧力一定で温度を上げると、液体から気体に状態が変わるという当たり前の現象をp-h線図で読むことができます。
エンタルピーHは
$$ dH = dU + PdV + VdP = dU + PdV $$
となります。dP=0ですね。
この例では液体から気体への状態変化を考えているので、dV=0ではありません。
dHはここで温度に比例することが分かります。
液体ではdV∝dTです。熱膨張の世界ですね。
気体の場合はPV=nRTの関係から、
$$ dH = dU + PdV = dU + nRdT $$
と表現できて温度Tで決まります。
単原子分子ならdU=3/2nRTと表現できるので、dH=5/2nRTです。ご参考まで。
熱のやり取り
次に熱のやり取りなしという条件を見てみましょう。
簡易的に記載します。
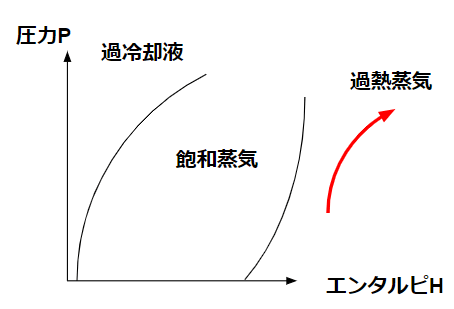
熱力学的には断熱変化と呼ぶ現象で、圧縮機での変化が相当します。
断熱変化で熱を外部とやり取りしない環境なら、圧力が上がると温度が上がるという感覚的な理解で十分です。
冷凍サイクルの温度とp-h線図(p-h diagram)
さて、それでは典型的な冷凍サイクルとp-h線図を重ねてみましょう。
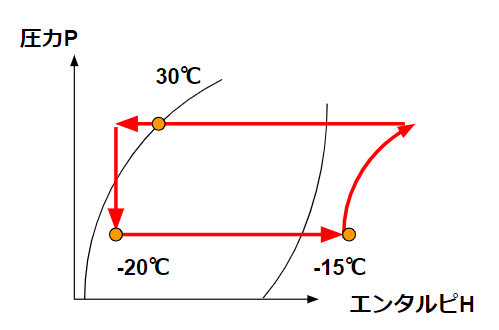
簡単に冷凍サイクルの状態を示すと以下の通りになります。
| 蒸発器 | 液体→気体 | -20℃ | -15℃ |
| 圧縮機 | 気体 | -15℃ | |
| 冷却器 | 気体→液体 | 30℃ | |
| 膨張弁 | 液体 | 25℃ | -20℃ |
温度はあくまでも例です。
蒸発器が冷凍機の機能として最も大事で、プロセス液を冷却させるための主要部分です。
ここがプロセス液より5℃程度低い状態になっていることでしょう。
この例ならプロセス液が-10℃前後まで冷やす冷凍機だということが分かります。
蒸発器という以上は出口で冷媒は蒸気になっています。
これを圧縮機で高圧・高温の状態に移行します。
凝縮器で冷媒を冷やして凝縮させます。
最後に膨張弁で圧力を開放させると、低温の状態に戻ります。
ここから見てわかるように、冷媒は蒸発器・凝縮器でそれぞれ必要な温度を得つつ、液体・気体の相変化をする物質と考えていいです。
この条件を満たしつつ、環境や安全性などを満足する媒体を探すことが冷媒の最大のミッションでしょう。それくらい難しいことです。
参考
冷凍機に関する本は非常に多いです。
実務上はそこまで使わないけども、体系的に理解したいという場合には、以下のような本が有用です。
関連記事
冷凍機について詳しく知りたい方は、以下の記事をご覧ください。
最後に
冷凍サイクルとp-h線図の基本を解説しました。
凍結サイクルの理解にはp-h線図が不可欠であり、冷媒の状態変化を視覚的に把握することで効率的な設備運用が可能になります。
初心者でも読み方を押さえれば、冷凍・空調設備のトラブル予防や性能改善に大いに役立ちます。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。(コメント欄はこの記事の最下部です。)
*いただいたコメント全て拝見し、真剣に回答させていただきます。


コメント