はりの曲げ応力(bending stress)の基礎式を解説します。
材料力学の基礎的な話です。
この内容が頭の中でしっかりイメージできると、プラント建屋設計や作業架台設計に直接効いてきます。
基礎式であるがゆえに、応用に幅広く使われます。
式展開も含めてゆっかり確認していきましょう。
少し難しい例としての、弾塑性変形も考えてみます。
曲げ応力(bending stress)の公式
はりの曲げの公式をまずは考えましょう。
曲げ応力で見ている場所
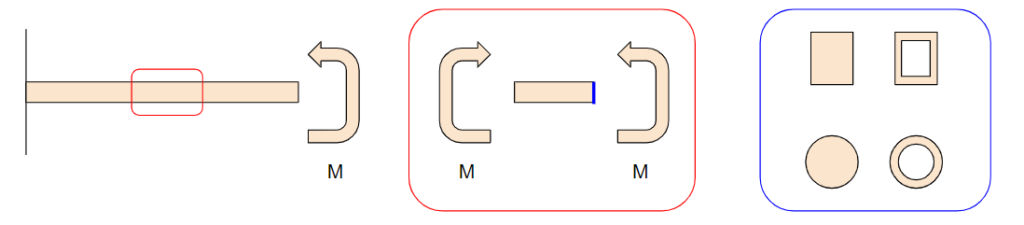
片持ちはりに曲げモーメントMが加わっている状態です。
この辺は教科書の図が結構わかりにくくて、理解に時間が掛かった記憶があります。
曲げモーメントが加わっているはりの一部を切り取ってみます。
赤で囲った部分です。
このはりの一部には左右に曲げモーメントMが加わっていると考えられます。
板を両手で曲げようとするときのイメージと同じ。
この曲げモーメントが加わているときに、はりの断面に加わる応力を計算しようというのが、曲げ応力の話です。
断面はいろいろな形状があります。
断面の青部分は、例えば四角形であったり円であったり、中が空洞であったりと、形状は様々。
プラント配管的には中空円が相当します。
建物であればH鋼や角柱です。
こうした断面形状に寄らずに、一律で同じ式でまとめるために、断面二次モーメントの考え方があります。
曲げ応力分布
さて、ここで断面は長方形の形状を考えましょう。
もっとも簡単です。
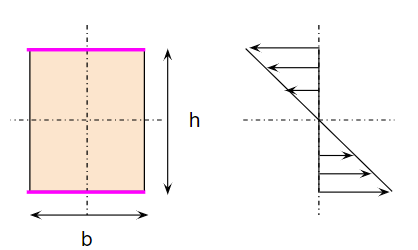
短辺b（幅方向）・長辺h（高さ方向）の長方形です。
この断面を持つはりに曲げモーメントが加わると、右のように高さ方向に対して応力の分布を持ちます。
中央部分は応力が働きません。
上下端では応力が最も大きくなります。
これを数式で示すと以下のようになります。
$$ M=\int_{A}yσ_xdA $$
この式は、断面に掛かる応力を断面で積分したらモーメントになるという関係を使っています。
良く分かりませんね。
曲げ応力σxは中央部が0で、高さ方向にズレた分だけ応力が比例関係で変わると考えます。
$$ σ_x=\frac{2σ_by}{h} $$
この関係が成立する変形を、弾性変形と言います。
これを使うと、
$$ M=\int_{A}yσ_xdA = \frac{2σ_b}{h}\int_{A}y^2dA $$
と表現できます。
この積分部分が断面二次モーメントIと呼ばれます。
長方形の今回の例だと
$$ I=\int_{A}y^2dA=\frac{1}{12}bh^3 $$
となります。
この式を使って、曲げ応力は以下のようにあらわすことが可能です。
$$ σ_x=\frac{M}{I}y $$
シンプルな表現になりました。
最大曲げ応力σbはy=h/2の時なので、
$$ σ_b=\frac{M}{I}\frac{h}{2}= \frac{6M}{bh^2} $$
と表現できます。
これが曲げ応力として一般に使われる式でしょう。
最大曲げ応力が材料の許容応力以下となるように、部材の選定や外力の設定などをしていきます。
非常に幅広く使われる式です。
イメージ
曲げ応力を考えるにあたって、はりの一部分を考えました。
これはイメージを簡単にします。
はりの一部分に曲げモーメントが加わると、はりは曲がります。
ここで微小な体積の梁を考える（長さを微小に区切る）と、はりは台形の形に変形します。
曲げ応力が弾性変形なら高さ方向に直線的に変わるからですね。
図の上側は圧縮され、下側は引っ張られます。
この微小区間を長さ方向に足していくと、はりが曲がっているように見えます。
弾塑性変形の場合
弾性変形の場合の曲げ応力の応用として、弾塑性変形の場合を考えましょう。
弾塑性変形は、弾性領域を越えた領域の話。
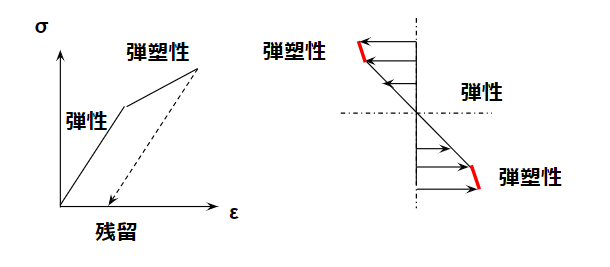
弾性変形では応力を加えると比例したひずみが発生します。
応力を取り除くとひずみは0になります。
ばねやゴムをちょっと伸ばして元に戻すイメージ。
ところが弾性領域を越えたさらに大きな応力を加えると、応力を取り除いてもひずみは0になりません。
この領域を弾塑性変形と言います。
複雑な応力-ひずみ曲線になりますが、簡単のために直線系で示します。
弾性領域の傾きと弾塑性領域の傾きを変えています。弾塑性の方が傾きが緩いケースです。
ここではり断面の曲げ応力分布は、はりの高さ方向に比例関係ではなくなります。
弾塑性変形の部分は、はりの断面の上下端部分になります。
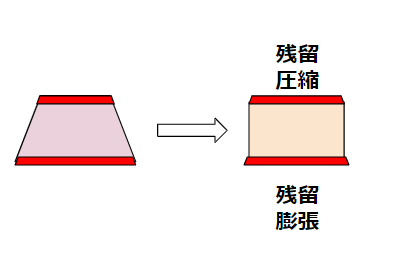
弾塑性変形でも変形量が微小な時には、ひずみは弾性変形と同じように線形関係と見なせます。
弾塑性領域の応力ひずみの傾きが小さいほど、ひずみが線形であれば応力は高い方向になります。
応力を開放しても、上下端のひずみの一部は残ります。
このままだといびつな形になりますが、弾性変形と同じように台形の形を維持しようとします。
その結果残留応力が働きます。
台形を維持できない程度の力が加わて力を開放すると、ひずみが弛みなどの現象として現れます。
曲げモーメントがさらに大きくなると、弾塑性変形領域が大きくなり、上下端に加わる曲げ応力が破断応力を越えます。
ここで材料は破断します。
針金などを曲げていくと、上下端面から割れるイメージと同じです。
圧縮よりも引張の方が弱いので、引っ張られる側から破断が起きるでしょう。
上下端面に一度亀裂が発生してしまうと、亀裂部に応力集中が起きて亀裂がどんどん進展していきます。
弾塑性変形領域を傾きがあるケースで考えましたが、もっと簡単に傾きゼロで考える方が分かりやすいかもしれません。弾塑性変形が起きた瞬間に、ひずみが無限大になるので即破断というイメージです。ビニール袋が弾塑性変形して亀裂が入った時には、このイメージに近いでしょう。勝手にどんどん破れていきますよね。
参考
材料力学は大学の専門で学んだとしても、実務で使うまでの間に時間が経って忘れてしまうと結構怖いです。
実務で使うためにも、以下のような本は捨てずに置いておきたいですね。
関連記事
材料力学についてさらに知りたい方は、以下の記事をご覧ください。
最後に
はりの曲げ応力の基本式を解説しました。
曲げ応力はどこの部分を示しているか分かりにくく、理解するのに時間が掛かります。
一度理解しても結果の式だけを使うことが多く、応用がなかなかできません。
弾塑性変形の例を考えるときに、この基礎の理解が役立ちます。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。） *いただいたコメント全て拝見し、真剣に回答させていただきます。