丸棒のねじり(twist)の基本式を求めます。
材料力学の範囲です。
梁の曲げ応力と同じく、弾塑性変形をかんたんに考えてみます。
なお、化学プラントの機電系エンジニアリングでは弾塑性変形のような深い知識はほとんど使いません。
単なるケーススタディ・練習という位置づけです。
あえて言うと、こういう応用的な考えは実務で役に立つ場合は多いです。
フックの法則
ねじりの基礎式を求めるためには、フックの法則を使います。
$$ τ=Gγ $$
τはせん断応力、Gは横弾性係数、γはせん断ひずみです。
これは材料力学でよく見かける式ですね。
せん断ひずみ
せん断ひずみを求めましょう。
以下のような丸棒をねじる場合を考えます。
この赤枠の部分を細かく見ていきましょう。
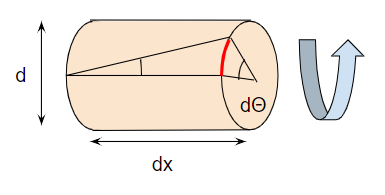
直径d、長さdxの部材にトルクTが掛かっています。
この結果、部材がねじる方向に微小に変形します。
ここで、比ねじれ角φを定義しましょう。
$$ φ=\frac{dΘ}{dx} $$
単位長さのねじれ角という意味です。
さて、比ねじれ角と使って棒内面のせん断ひずみを見ていきましょう。
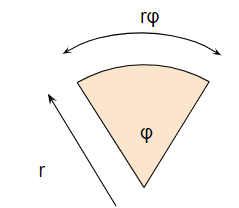
弾性変形においては断面の比ねじれ角はφで一定です。
半径rと比ねじれ角を使えば、せん断ひずみに相当する弧の長さを以下のように表現できます。
$$ γ=rφ $$
ねじりモーメント(twist)
せん断ひずみが求まると、ねじりモーメントを求めることができます。
丸棒にトルクTが掛かっている時、丸棒断面の半径rの円部分にはrφというせん断ひずみが周上に働いています。
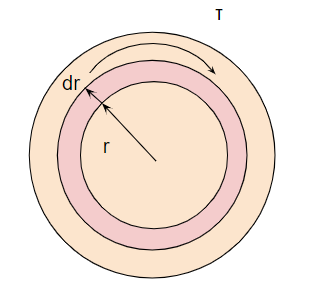
この領域に作用するトルクdTは以下のように表現できます。
$$ dT=rdτ=rGγdA=rGrφ2πrdr $$
トルクが距離×せん断応力であることに注意しましょう。
これをr方向に積分を取ると、丸棒全体に働くトルクとなります。
$$ T= 2πGφ\int_{0}^{d/2}r^3dr = \frac{1}{32}πGφd^4$$
ねじれ角
上記トルクの式から、比ねじれ角φは
$$ φ=\frac{32T}{πGd^4}$$
と表現できます。
丸棒の長さをLとすれば、単にLを掛けたものがなじれ角になります。
$$ \frac{32LT}{πGd^4}$$
弾塑性変形の場合（せん断応力一定）
ここで弾塑性変形の場合を少し考えましょう。
半径r1以降は塑性変形をすると仮定します。
せん断応力は弾性変形と等しいとしましょう。
つまり、以下のような状況を考えることになります。
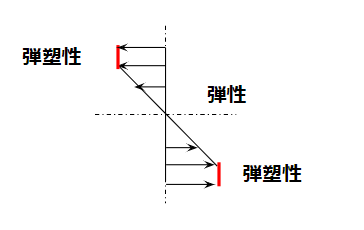
弾性変形部分は、上で紹介した式と同じ形になります。
$$ T_1=\frac{1}{2}πGφ_1r_1^4$$
半径r1以降の外面部は塑性変形です。
ここでせん断応力が一定という条件が入ります。
$$ τ_2=Gr_1φ_1=const. $$
半径r1以降の外面部のトルクは以下のように表現できます。
$$ T_2= 2πGr_1φ_1\int_{r_1}^{d/2}r^2dr = \frac{2}{3}πGr_1φ_1(\frac{1}{8}d^3-r_1^3)$$
トルクTはT1とT2を足し合わせたものなので、以下の通りになります。
$$ T=T_1+T_2=πGr_1φ_1(\frac{1}{12}d^3-\frac{1}{6}r_1^3)$$
せん断応力一定と仮定した場合は、せん断ひずみがr1で最大となり半径方向のねじれ角も奇妙な状況となります。
せん断ひずみ一定と仮定した場合は、やはり半径方向のねじれ角がr1で最大になる奇妙な形をするでしょう。
実際には塑性変形段階でも応力やひずみも変化があるので、丸棒の外周部が最も変形量が多く、最初に破断するというイメージの方が正しいと思います。
曲げ応力の時と比べて半径の要素が入ってくるので、状況が複雑になるということが分かればOKだと思います。
参考
材料力学は大学の専門で学んだとしても、実務で使うまでの間に時間が経って忘れてしまうと結構怖いです。
実務で使うためにも、以下のような本は捨てずに置いておきたいですね。
関連記事
ねじりを含む材料力学は機械系の必須科目です。
化学プラントの機械設計者でもこれは同じです。
さらに知りたい方は、以下の記事をご覧ください。
最後に
丸棒のねじりの基礎式を求めてみました。
フックの法則・ねじれ角・トルクという関係を使って、積分で求めていきます。
対象としている系のイメージさえ分かれば、式はさほど難しくはありません。
弾塑性変形の場合も仮定を置いて少し考えてみました。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。） *いただいたコメント全て拝見し、真剣に回答させていただきます。
コメント