振動の時間応答と周波数応答のイメージ|共振周波数はすぐに回避

　振動工学では周波数応答を中心に議論がなされます。時間応答の方がイメージしやすいのに、周波数応答で議論していくうちに、実際に動くイメージが後回しになってしまいがちです。実験や現場で現象を確認すれば補正はできるのですが、できれば机上勉強段階でイメージしたいもの。
　本記事では振動の時間応答と周波数応答の間をつなぐ解説をします。

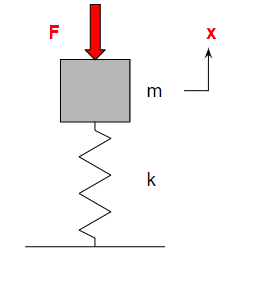
1自由度系モデル

振動の基礎的な式である1自由度系モデルを考えます。運動方程式と周波数応答は以下の通りに与えられます。

$$ m\ddot{x}+kx = 0 $$

$$ Fe^{iωt} $$

$$ X=X_0\frac{1}{1-(\frac{ω}{ω_0})^2} $$

モデルと時間応答・周波数応答のグラフも示します。

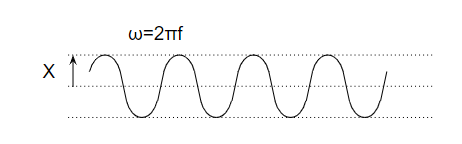
変位の時間応答

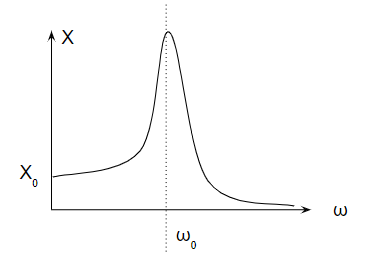
変位/力の周波数応答

力と変位の時間応答

周波数応答は力と変位の絶対値の関係を示しています。周波数が異なれば、変位が変わるということを上の周波数応答のグラフは示しています。例えば、質点mにある周波数ωの力Fが加わるとします。この場合の質点mの変位Xは以下のようになるでしょう。

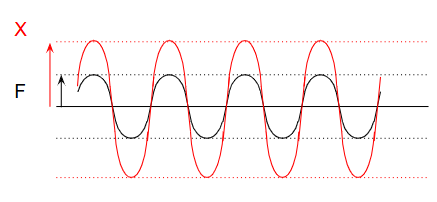
力Fの絶対値は変えなくても周波数ωが変わると、変位Xは変わります。例えば以下のような形になります。

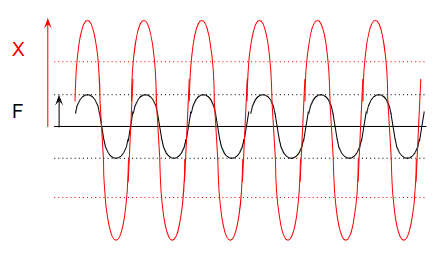
周波数が高い（振動数が高い）と変位Xが大きくなる様を示しています。周波数応答でもω=ω₀までは周波数が上がるとこの関係どおりです。ω=ω₀になると変位が∞となり、質点がその場所を維持できずに例えばバネが壊れるなどの問題が現実には起こります。ω₀を越えると、変位は小さくなっていくことも1つのポイントです。

安定した変位

実際の振動機器の動きを見ると、上のような時間応答の図はやや奇妙です。現実には以下のような形になります。

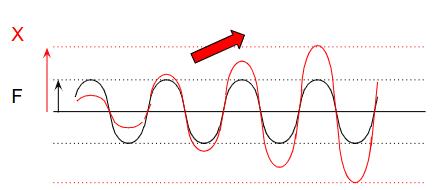
動き初めは変位が小さく、時間が経つにつれて変位が増えて一定値になる。この一定値が常時繰り返されているのが先に示した時間応答のグラフです。

これは粘性というファクターが入っているからで、粘性が無視できる系では力を加えた瞬間に常時の時間応答のグラフの形に移行するでしょう。

早く周波数を変える

ω=ω₀になると共振と呼ばれる状態で、設備が壊れるため危険といわれます。対策は共振周波数から早く逃げること、といわれます。これは力Fがすぐに目的の回転数に到達しない設備をイメージしています。

　例えばポンプのモーターであれば、起動後にすぐに目的回転数に到達するでしょう。一方で、大きな振動機器になると設備を動かすために大きなエネルギーが必要で、目的回転数に到達するまで一定の時間が掛かります。目的回転数に到達するまでに共振周波数が存在するので、共振が来て問題だという主張です。これをグラフで見てみましょう。

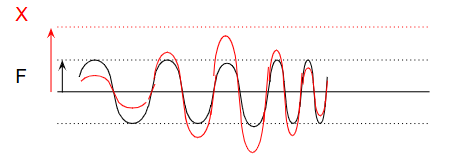
力Fは周波数ωのサインカーブですが、時間が経つにつれて周波数が高くなります。この力Fに応じて変位Xは変化します。同じ周波数で動いていても到達変位までに時間が掛かりますが、周波数を変えている間にも変位は時々刻々変化します。共振周波数に到達したからといって、すぐに共振変位（例えば∞）に到達するわけではないので、速やかにもっと高い周波数に移行することで、変位Xが高くならないように、ということが言いたいわけですね。

参考

最後に

• 時間応答は「現実の動き方」、周波数応答は「力と変位の関係」を示すもの。
• ω=ω₀ 付近では変位が極端に大きくなる（共振）ため注意が必要。
• 粘性を考慮すると、現実の時間応答は徐々に安定していく。
• 設備の起動時は、共振周波数を素早く通過することで破損を防げる。

時間応答と周波数応答を結びつけて理解することで、机上での設計と実機の挙動をより正確にイメージできるようになります。

化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）X（旧Twitter）のDMでも可能です。

• 設備設計で悩んでいる
• トラブル原因の考え方が分からない
• 若手の教育方法に困っている

など、幅広くお受けしています。
*いただいたコメント全て拝見し、数日中に真剣に回答させていただきます。

ブロトピ：今日のブログ更新