質点付き梁の運動方程式を解説｜振動工学の拡張モデルを理解する

　梁の振動方程式は振動工学で広く使われます。とくに有名な片持ち梁の運動方程式はそれだけでも使う機会は多いですが、使う機会を増やそうとすると自由度を上げる必要があります。
　本記事では梁の1点に質点とばねを加えたときの運動方程式の考え方を紹介します。実際には数値計算をして確かめることになりますが、概念が分かっていないと検証ができませんからね。

運動方程式

まずは運動方程式を立てることを考えましょう。梁だけの運動方程式は以下のように記載できます。

$$ ρA\frac{\partial^2 y(x,t) }{\partial t^2 }+EI\frac{\partial^4 y(x,t) }{\partial x^4 } = f(x,t) $$

ここに質点を1つ加えます。イメージは以下の通りです。

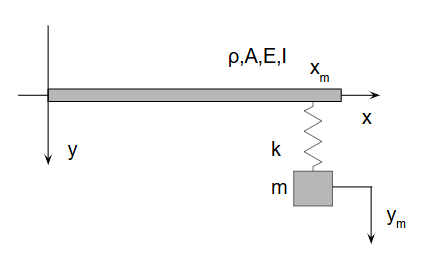
この場合の運動方程式は以下のようになります。梁と質点を分けて記載しています。

$$ ρA\frac{\partial^2 y(x,t) }{\partial t^2 }+EI\frac{\partial^4 y(x,t) }{\partial x^4 } = k(y_m(t)-y(x_m,t)) $$

$$ m\frac{\partial^2 y_m(t) }{\partial t^2 } = -k(y_m(t)-y(x_m,t)) $$

梁のx_mという位置に質点mが加わっていて、質点mはy_m(t)という変位です。x_mの位置の梁の変位はy(x_m,t)です。

運動方程式の変形

梁と質点の運動方程式を足し合わせましょう。ばね力の部分が相殺されます。

$$ ρA\frac{\partial^2 y(x,t) }{\partial t^2 }+EI\frac{\partial^4 y(x,t) }{\partial x^4 }+m\frac{\partial^2 y_m(t) }{\partial t^2 } = 0 $$

ここでy(x,t)は、現実的には以下のように表現されることに注目しましょう。連続体ではあるものの、実際には接点nの離散値として扱うので、n個の運動方程式を集約した表現と解釈できます。

$$ \mathbf{y(x,t)}=\begin{pmatrix} y_{1}(t) \\ \dots \\ y_{n}(t) \end{pmatrix} $$

変数分離しようとしたら、以下のような表現になります。

$$ \mathbf{y(x,t)}=\begin{pmatrix} ψ_{11} & ψ_{12} & \dots & ψ_{1n} \\ \dots \\ ψ_{n1} & ψ_{n2} & \dots & ψ_{nn} & \end{pmatrix} \begin{pmatrix} φ_{1}(t) \\ \dots \\ φ_{n}(t) \end{pmatrix}$$

質点mが加わった運動方程式もn+1個の運動方程式と考えると、同じような表現が可能です。

$$ ρA\frac{\partial^2 y'(x,t) }{\partial t^2 }+EI\frac{\partial^4 y'(x,t) }{\partial x^4 } = 0 $$

$$ \mathbf{y'(x,t)}=\begin{pmatrix} y_{1}(t) \\ \dots \\ y_{n}(t) \\ \color{red}{y_{m}(t)} \end{pmatrix} $$

一番最後の行にy_m(t)が加わっていることがポイントですね。同じく変数分離を意識した表現を見てみましょう。

$$ \mathbf{y'(x,t)}=\begin{pmatrix} ψ_{11} & ψ_{12} & \dots & ψ_{1n} & ψ_{1m}\\ \dots \\ ψ_{n1} & ψ_{n2} & \dots & ψ_{nn} & ψ_{nm} \\ψ_{m1} & ψ_{m2} & \dots & ψ_{mn}& m/ρAψ_{mm} \end{pmatrix} \begin{pmatrix} φ_{1}(t) \\ \dots \\ φ_{n}(t) \\ \color{red}{φ_{m}(t)} \end{pmatrix}$$

考察

こういう式を見たときに考えることは、追加した要素のパラメータが変わった時にどういう式になるかを考えることです。

m=0

m=0つまり質点が無い場合を考えましょう。この場合、一番下の行は全く意味がなく、質点が無い時の運動方程式と等しくなります。当たり前のことですが、忘れないでチェックすることが大事です。

m=∞

m=∞つまり質点が動く物ではなく固定されている状態を考えましょう。これは両端固定などの運動方程式と同じことが予想されます。

位置x_mという表現は分かりにくいので、自由端である末端nに質点mが位置していると考えてみましょう。y(x,t)は以下のように表現されます。

$$ \mathbf{y'(x,t)}=\begin{pmatrix} ψ_{11} & ψ_{12} & \dots & ψ_{1n} \\ \dots \\ ψ_{n1} & ψ_{n2} & \dots & (1+m/ρA)ψ_{nn} \end{pmatrix} \begin{pmatrix} φ_{1}(t) \\ \dots \\ φ_{n}(t) \\ \end{pmatrix}$$

m=∞だと一番最後の行がまた意味を持たない結果になります。n-1個の運動方程式を考えて、n番目の接点は境界条件を与えて計算することになります。質点mが別の位置にあっても考え方は同じです。

ψ(x)は固有モードを意味しますので、質点mの位置が変わることで固有モードが変わるのは当たり前ですよね。梁の運動方程式の立て方を考えると、微小区間に分割して積分していくので、質点mが位置する接点の両隣の接点と相互作用が発生します。この部分が固有モードを変形させる要因となります。

参考

最後に

質点やばねを加えた梁の運動方程式は、単純な片持ち梁よりも自由度が高く、現実の構造に近いモデルです。

• 梁と質点の相互作用を考慮することで、より正確な振動挙動を再現できる
• m=0 や m=∞ のケースを比較すると、境界条件との対応関係が理解しやすい
• 質点位置の違いが固有モードを変形させる

このような考え方を理解しておくことで、実際の構造解析や数値シミュレーションでも理論と結果を正しく結びつけることができます。

化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。）X（旧Twitter）のDMでも可能です。

• 設備設計で悩んでいる
• トラブル原因の考え方が分からない
• 若手の教育方法に困っている

など、幅広くお受けしています。
*いただいたコメント全て拝見し、数日中に真剣に回答させていただきます。

ブロトピ：今日のブログ更新