架台は、設備や機器を支える重要な構造物です。その強度が不足すると、安全面で大きなリスクを伴います。
本記事では、架台の強度計算の基本的な考え方から、実務で押さえておきたいポイントまでわかりやすく解説します。
初心者のエンジニアや設計担当者が、まず理解しておくべき内容に絞っていますので、ぜひ参考にしてください。建屋を設計するときは専門の強度計算を行いますが、架台レベルだと詳細計算をすることはほぼありません。既存と同じ構造や部材を選定していれば、とりあえずOKですからね。
変に強度計算で部材を削減しようとしても、コストメリットが出ずに危ない状況になるくらいなら、1サイズ上げておこう。こういう発想で、設計を省力化します。
とはいえ、計算方法の概要を知らなければ、エンジニアとしてはちょっともったいない気もします。どういう考えで設計されているかを知ることは、臨機応変な対応をするうえで役経つことでしょう。
この記事は、荷重シリーズの一部です。
タンク設計の基礎:風荷重と地震荷重の計算事例で学ぶ
機器荷重・ローディングデータの考え方|化学プラントの土木建築設計
パイプスタンドの強度計算と長期荷重・短期荷重
パイプスタンドの強度計算がこれで分かる!
配管サポートの強度計算を材料力学的に考える
安易なラック継ぎ足しが招く落とし穴――強度・作業性・保守性の観点から考える配管設計の注意点
モデル
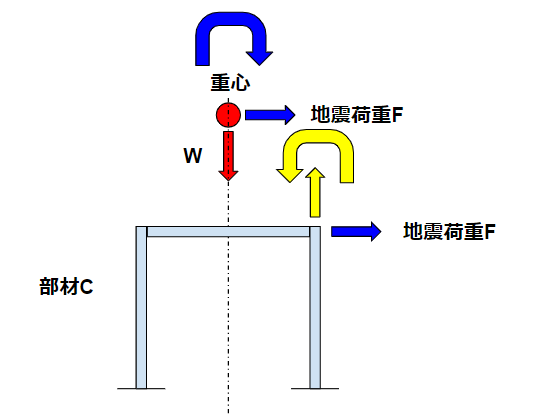
今回考えるモデルは以下の通りです。
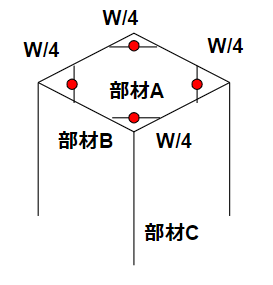
これが、いわゆる架台です。
4本足で真ん中にタンクや反応器などをセットして、架台の水平リブに相当する火打ち梁で設備の荷重を受けます。
設備はブラケットで支持します。設備の重量をWとします。
梁の強度計算
架台の強度計算の最初のステップは梁の強度計算です。
部材Aの火打ち梁は、材料力学の基礎式そのものを適用します。
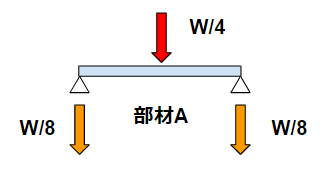
両端支持・梁の真ん中にW/4(火打ち梁が4本あるから)として梁のたわみ計算をします。
これで梁のたわみ・曲げ応力が許容値以下になるように、部材の選定をします。
断面2次モーメントを上げていきます。
部材Aで受けた荷重はそのまま部材Bに伝達されます。
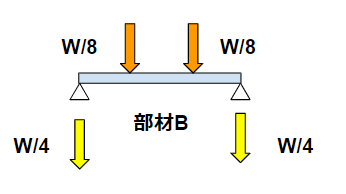
部材Bも部材Aと同じ梁のたわみ計算をします。
荷重が掛かる位置が部材Aとは少し違いますので、注意がやや必要です。
部材Bも大きさも部材Aと同じように計算しますが、部材Bの方が一般には長いので、大きな部材が必要になります。
部材Bで受けた垂直荷重は、架台の柱部分である部材Cに伝達されます。
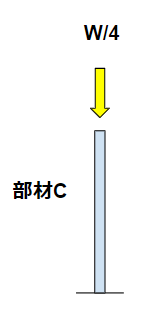
部材Cとしては、座屈の計算を行います。
これも材料力学の基礎的な話です。
地震荷重の計算
強度計算上は地震荷重を考えないといけません。
地震により設備が水平方向に移動して、それを受けるための荷重として地震荷重なる物を考えます。
地震荷重そのものは係数によります。
(設備の荷重)×(地震係数)=地震荷重
という発想です。
地震係数なるものは、地域・計算基準などによって変わります。
部材Cには地震によって水平荷重と垂直荷重の2つが発生します。
水平荷重:設備の地震荷重そのもの
垂直荷重:設備の地震荷重と重心差から発生するモーメントに抵抗するモーメント
水平荷重は分かりやすいでしょう。
垂直荷重はやや分かりにくいでしょう。
(設備の重心-架台の部材A・Bの高さ)×(地震荷重)=(部材Bの長さ)×(垂直荷重)
という計算になります。
タンクの重心位置とブラケット位置が近い方が良い、という理由はここにあります。
左辺がほぼゼロになって、垂直荷重を考慮する必要が無くなってきます。
垂直荷重も梁のたわみ計算を行って評価します。
部材Cとしては設備荷重による座屈と地震荷重によるたわみを考慮して、両方とも満足する部材を選定します。
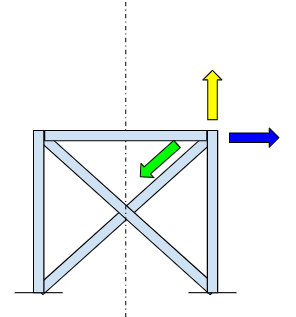
斜材を付けた場合は、部材Cの水平荷重と垂直荷重を緩和する方向になります。
下の図のようなイメージで捉えていると良いでしょう。
取付ボルト
取付ボルトは部材Cに掛かる力・モーメントから計算をします。
考え方はアンカーボルトの計算とほぼ同じです。
梁に掛かる応力は水平応力と垂直応力の複合計算であることに注意しましょう。
数式を使った理解
ざっくり理解と言いつつ、数式を使った理解も最後に示します。
なお、以下の条件は共通して使います。
M:曲げモーメント
σ:曲げ応力
Z:断面係数
添え字のA,B,C・・・は部材のA,B,Cを示す
部材A
部材Aの梁の曲げ応力を計算します。
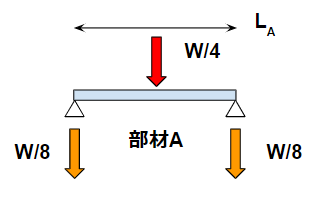
荷重W/4、長さLA、両端支持の式を使います。
$$ M_A=\frac{W}{4}\frac{L_A}{2}\frac{1}{2} = \frac{WL_A}{16} $$
$$ σ_A=\frac{M_A}{Z_A} = \frac{WL_A}{16Z_A} $$
部材B
部材Bも部材Aと同じように計算します。
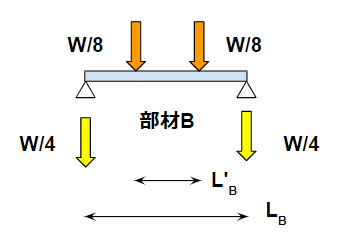
$$ M_B=\frac{W}{8}\frac{L_B-L’_B}{2}= \frac{W(L_B-L’_B)}{16} $$
$$ σ_B=\frac{M_B}{Z_B} =\frac{W(L_B-L’_B)}{16Z_B} $$
部材C
部材Cについて見ていきます。
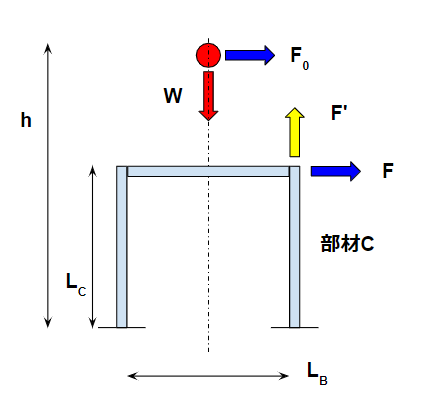
地震荷重Fについて部材Cでも水平荷重としてFは作用します。
$$ F=\frac{1}{2}F_0 $$
一方で、高さ差によるモーメントを受けるため、垂直荷重も受けます。これをF’とすると、
$$ F’\frac{L_B}{2} = F_0(h-L_C) $$
$$ F’=\frac{h-L_C}{L_B}F $$
部材D
部材Dがある場合も考えましょう。
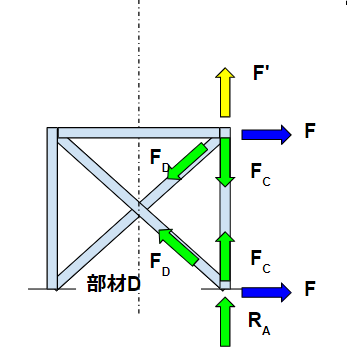
こんな感じで、斜材の部材Dが入った場合は式が若干複雑になります。
力の釣り合いを考えると(正負の記号は適当に付けています)、鉛直方向・水平方向それぞれ以下の通りになります。
$$ F_D\frac{L_C}{L_D}+F_C-F’=0 $$
$$ F_D\frac{L_B}{L_D}-F=0 $$
これらの式から、以下の通りとなります。
$$ F_D=F\frac{L_D}{L_B} $$
$$ R_A=F’=\frac{h-L_C}{L_B}F $$
部材Cの断面積をAとすると、部材Cの固定点に掛かる引張応力、せん断応力はそれぞれ
$$ σ_k=\frac{R_A}{A} $$
$$ τ_k=\frac{F}{A} $$
となり、これらを主応力σmを計算すると
$$ σ_m=\frac{1}{2}σ_k+\frac{1}{2}\sqrt{{σ_k}^2+4{τ_k}^2} $$
となります。
参考
関連記事
架台の強度計算を詳しく知りたい方は、以下の記事も合わせてご覧ください。
最後に
架台は、プラントや設備の安全稼働に欠かせない構造物です。強度計算は荷重や材料強度、安全率をしっかり考慮し、設計の信頼性を確保します。初心者はまず基本的な荷重の種類や計算目的を理解し、実務では設計基準や現場条件を踏まえた応用力を磨くことが重要です。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。(コメント欄はこの記事の最下部です。)
*いただいたコメント全て拝見し、真剣に回答させていただきます。


コメント
お世話になっております。
ご返信が遅くなり、申し訳ございません。
現在、大変恐縮ですが、お電話でのご相談は対応を見合わせております。