本文将详细讲解双自由度振动系统的基本概念与计算方法。
在学习完单自由度系统后，你可能会觉得“双自由度”只是多了一个质量块而已，但其实复杂度会显著提升。
这一主题虽然在化工厂的日常工作中不常直接使用，但理解它能帮助工程师在设备设计、支撑结构或振动控制方面建立更深入的直觉。
双自由度振动系统模型
让我们先看双自由度振动系统的基本模型。
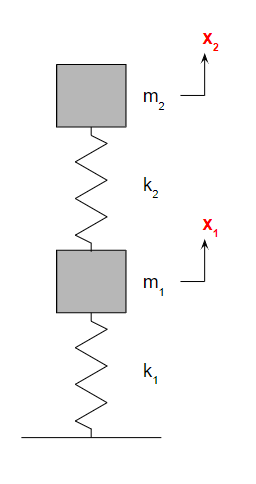
双自由度振动系统看起来像两个单自由度系统串联而成。
系统由两个质量块 m1,m2、两个弹簧常数 k1,k2、以及位移 x1,x2 组成。
运动方程
假设外力 FFF 只作用在 x1一侧。
$$ m_1\ddot{x_1}+k_1x_1 = f+k_2(x_2-x_1) $$
$$ m_2\ddot{x_2} = -k_2(x_2-x_1) $$
则系统的运动方程如下：
$$ m_1\ddot{x_1}+(k_1+k_2)x_1-k_2x_2 = f $$
$$ m_2\ddot{x_2}+k_2(x_2-x_1) = 0 $$
要注意弹簧回复力方向的符号。当 x2 相对于 x1 向正方向移动时，弹簧 k2 被拉伸，并产生相反方向的回复力。
求解过程
假设解的形式为：
$$ x_1=X_1e^{iωt} $$
$$ x_2=X_2e^{iωt} $$
$$ f=Fe^{iωt} $$
代入上式得到：
$$ (1+\frac{k_2}{k_1}-\frac{m_1}{k_1}ω^2)(1-\frac{m_2}{k_2}ω^2)k_1X_2-\frac{k_2}{k_1}k_1X_2 = F $$
从第二式可以求出 X1 与 X2 的关系式，并最终得到系统的频率响应表达式。
$$ X_2=\frac{F}{k_1}\frac{1}{(1+φ-(\frac{ω}{ω_1})^2)(1-(\frac{ω}{ω_2})^2))-φ} $$
$$ X_1=\frac{F}{k_1}\frac{1-(\frac{ω}{ω_2})^2}{(1+φ-(\frac{ω}{ω_1})^2)(1-(\frac{ω}{ω_2})^2))-φ} $$
物理意义与解释
1. 参数 φ 的意义
表示两个弹簧刚度的比值。
当 φ=0 时，系统退化为单自由度模型。
当 φ → ∞ 时，表示两个质量块的位移相同 。
2. 固有频率 ω₁、ω₂
它们分别表示系统的第一、第二阶固有频率。
这两个频率对应系统振动响应的两个“共振峰”。
3. X₁、X₂ 的行为
当 ω = ω₂ 时，X1=0，即受力点不动但 X2 振动最大。
这种现象称为振动隔离或减振（制振），是实际工程中常见的控制思想。
4. 频率响应
与单自由度系统只有一个共振峰不同，双自由度系统会出现两个峰值。
自由度的数量等于共振峰的数量，这是理解多自由度系统的关键。
总结（まとめ）
本文解析了双自由度振动系统的建模、运动方程与解的物理意义。
可以看到，自由度的增加会带来更多的共振点与复杂的动态耦合关系。
在化工设备设计与结构支撑分析中，理解这种多自由度特性，有助于避免共振与疲劳问题。
评论