在化工厂或反应釜的设计中,搅拌功率(Mixing Power) 是决定混合效率与能耗的重要指标。
很多工程师知道它的公式,却不太清楚公式背后的物理意义。
本文将以简单易懂的方式介绍:
- 搅拌功率的基本组成
- 雷诺数与功率数的关系
- 电机与机械功率之间的区别
学会这些基础概念,你就能在现场快速估算电机功率,优化设计,提高能源利用率。
搅拌器设计基础:单位体积搅拌功率(Pv)与电机功率的关系
搅拌器轴强度计算入门指南
什么是搅拌器的临界转速?——共振原理与实用计算方法
1. 搅拌功率的组成
所谓“所需搅拌功率”,实际上分为两个部分:
1️⃣ 机械功率:叶轮在液体中的实际做功;
2️⃣ 电气功率:电机与减速机提供的输入功率。
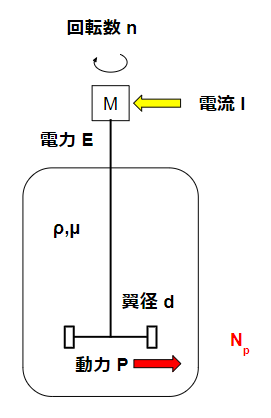
很多人只计算机械部分,而忽略了传动效率的损耗。
为了更直观理解,我们从“液体端的功率”出发,再回溯到电机输入端。
2. 雷诺数的计算
搅拌流动状态由 雷诺数(Re) 决定,公式如下:
$$ Re=\frac{d^2Nρ}{μ} $$
其中:
- d:叶轮直径
- N:转速(rps)
- ρ:液体密度
- μ:液体黏度
当 Re 较小时,为层流;较大时为湍流。
不同流态下,功率数(Np)的取值也不同。
在放大设计时,如果叶轮直径增大,为保持相同流态,需降低转速。
3. 净搅拌功率公式
基础公式为:
$$ P=N_pρN^3d^5 $$
说明:
- Np:功率数(与叶轮类型、流态有关)
- ρ:密度
- N:转速
- d:叶轮直径
功率与转速的三次方、叶轮直径的五次方成正比。
也就是说,直径稍微增大,功率就会大幅上升——放大设计时必须注意!
4. 功率数 Np 的意义
功率数(Np) 是一个经验参数,用来描述不同叶轮在不同流态下的能量消耗。
例如著名的 Nagata 经验式:
- 在低雷诺数下(粘性区),Np 随 Re 增大而急剧下降;
- 在高雷诺数下(湍流区),Np 趋于常数。
不同叶轮(如 Rushton 涡轮桨、倾斜叶片桨、螺旋桨式)都有特定的 Np–Re 曲线。
5. 为什么是 N³·d⁵?
从物理角度来看:
功率 = 力 × 速度
叶轮对液体施加的力与动量变化成正比: F∝ρ(Nd)2d2=ρN2d4F \propto \rho (N d)^2 d^2 = \rho N^2 d^4F∝ρ(Nd)2d2=ρN2d4
再乘以叶尖速度 Nd: P∝ρN3d5P \propto \rho N^3 d^5P∝ρN3d5
因此,公式中的指数来源于动量守恒与尺度分析,而非纯粹经验。
6. 系统损耗的考虑
上式计算的是 净搅拌功率,并非电机输入功率。
还需考虑电机与减速机的效率:
$$ E=\frac{P}{η_1η_2} $$
假设 η₁ = 0.9(电机效率),η₂ = 0.8(减速机效率),
则:
$$ E=\frac{P}{0.72} =1.38P$$
意味着实际所需电功率比理论值高约 38%。
7. 电流与负载的关系
电机输入功率公式为:
$$ E=\sqrt{3}VIcosφ $$
其中:
- V:电压
- I:电流
- cosφ:功率因数
在电压与功率因数基本不变的情况下,电流大小直接反映搅拌负载。
使用变频器调速时,可通过监测电流判断搅拌功率变化趋势。
总结(まとめ)
本文介绍了搅拌功率计算的核心原理,包括:
| 项目 | 公式 | 作用 |
|---|---|---|
| 雷诺数 | $$ Re=\frac{d^2Nρ}{μ} $$ | 判断流态 |
| 功率公式 | $$ P=N_pρN^3d^5 $$ | 计算净功率 |
| 效率换算 | $$ E=\frac{P}{η_1η_2} $$ | 计算电机输入功率 |
掌握这些基础后,你可以:
✅ 快速估算电机功率
✅ 优化搅拌器设计,提高能效
✅ 与电气、机械工程师更高效协作
记住:搅拌不仅是机械运动,更是能量传递过程。
理解功率的本质,才能真正做到“高效混合”。
作者简介 – NEONEEET
在化工行业工作20年以上,作为用户侧工程师贯通经历了设计 → 生产 → 设备保全 → 企划的全流程。 专注分享真正能在现场使用的批量化工实务知识。 → 查看完整简介

评论