柱の座屈について解説します。材料力学の基本的な範囲に限定します。柱の設計はプラント建物以外にも架台やサポートなどその範囲は広いです。
梁のたわみについてはイメージを持ちやすいですが、座屈はあまりイメージを持ちにくく難しいと感じるでしょう。
必要な考え方だけをピックアップしてみます。
材料力学上の計算
柱の座屈は材料力学の範囲で学習します。
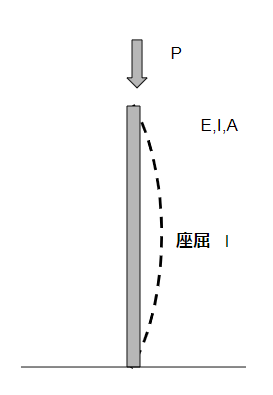
図のような柱の上部に力が加わっている状況を考えましょう。
力が弱い時には、柱はビクともしません。
力を加えていくと、あるタイミングで柱は図のように撓みます。
これは日常生活でも例えば、紙や本を両側から押したときに撓む形でイメージできるでしょう。
これを座屈と言います。
計算式はオイラーの理論式という式から、以下のように決まります。
$$ P=n\frac{π^2EI}{l^2} $$
Eはヤング率、Iは断面二次モーメント、lは長さという材料力学のいつもの諸元です。
nが境界条件によって決まる係数です。
| 境界条件 | n |
|---|---|
| 固定-自由 | 1/4 |
| 回転-回転 | 1 |
| 固定-移動 | 1 |
| 固定-回転 | 2.046 |
| 固定-固定 | 4 |
工学的に対象となる座屈を考えるとnは境界条件で決まります。
この式から求まる力を、断面積Aで割ったものが、座屈応力です。
$$ σ=\frac{P}{A} $$
このσが降伏応力より高いと座屈によって材料が破断します。
振動モードと同じ
少し脱線します。
座屈自体は境界条件だけで決まるわけではなく、力が上がるほど座屈の形が変わっていきます。
考え方は梁の振動モードと同じです。
力が大きいほど、柱も複雑な変形をします。
一番簡単な1次モードの変形が一番力が弱いです。
座屈応力 < 降伏応力
という関係を考えると、一次モードのみに着目したら良いでしょう。
実務で考えること
柱の座屈は上記の式で計算しますが、実務上は多少係数を乗せるでしょう。
例えば、地震荷重を短期長期で考えたり、プラントの運転条件で多少の係数を乗せます。
耐震計算は年々厳しくなるので、当時はその計算でよかったけども今の計算では不足するということも往々にしてありえます。
高い目に計算しておいて損はないでしょう。
私は機械エンジニアですので、建物の計算としての柱の座屈は計算しませんが、架台やサポートでは計算しています。
この場合には、境界条件n=1(固定-移動)としますが、安全係数として4くらいを入れています。
結果的に、固定-固定の条件と変わらなくなりますね。
毎回座屈の計算をしているわけではなく、既存の設備の大きさや部材を見て計算することもとても多いです。
むしろ計算する方が少ないくらいです。
柱の長さlや荷重Pが既存設備よりも条件が厳しい側の設計になるのであれば、部材を1サイズ上げておしまい。
既存プラントでプラント全体の大きさや配管の大きさが極端に変わることはなく、既存でOKであれば大抵はOKです。
古いプラントであれば1サイズ上げよう、新しいプラントなら同じ部材にしよう。
こんな感じで設計時間を短縮させています。
参考
関連記事
さらに知りたい方は、以下の記事をご覧ください。
最後に
プラントの建物・架台・サポートなどに使う柱の座屈計算の基礎を紹介しました。
材料力学を使います。
境界条件を決めて座屈応力と降伏応力を比較します。
実務的にはこの計算よりも、既存設備との比較をする方が速いでしょう。
長さlや荷重Pを適切に見極めましょう。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。(コメント欄はこの記事の最下部です。)
*いただいたコメント全て拝見し、真剣に回答させていただきます。
この記事の内容を、あなたの職場・キャリアに合わせて整理したい方に技術・キャリア相談を行っています。海外プラント、製造管理、組織の病理、キャリア停滞など、あなたの状況に合わせて具体的にアドバイスします
→ 技術・キャリア相談はこちら
【著者:ねおにーーと】
化学プラントで20年以上、設計→製造→保全→企画まで一気通貫で経験したユーザー側エンジニア。 バッチプラントの設備・運転・トラブル対応を中心に、現場で本当に役立つ知識を発信しています。 → 詳しいプロフィールはこちら


コメント