Let’s take a closer look at two-degree-of-freedom (2-DOF) vibration systems.
If there is a one-degree-of-freedom (1-DOF) system, it’s natural to think a 2-DOF version should exist as well.
At first glance, it might seem like just adding another “1.”
But in reality, the complexity increases dramatically.
In chemical plants, mechanical engineers rarely need to use this theory in daily work.
However, understanding 2-DOF vibration models helps you grasp the essence of vibration control and the physical meaning behind system responses — a key point that separates mechanical knowledge from simple “tool handling.”
This article is part of the vibration analysis series:
- Overview of the 1-DOF vibration system
- Beam vibration equations explained
- Vibrating beams with attached mass
- Effects of machinery vibration on structures
- Understanding time and frequency response
Model of a Two-Degree-of-Freedom System
The 2-DOF vibration model can be seen as two 1-DOF systems stacked together.
Each has its own mass (m), spring constant (k), and displacement (x).
We use subscripts “1” and “2” to distinguish them.
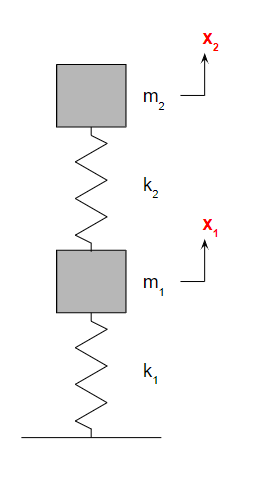
As noted in the 1-DOF article, building this kind of model physically with actual springs and weights is quite challenging — but conceptually, it’s straightforward.
Equations of Motion
Assume the external force F acts only on mass 1.
The motion equations are:
$$ m_1\ddot{x_1}+k_1x_1 = f+k_2(x_2-x_1) $$
$$ m_2\ddot{x_2} = -k_2(x_2-x_1) $$
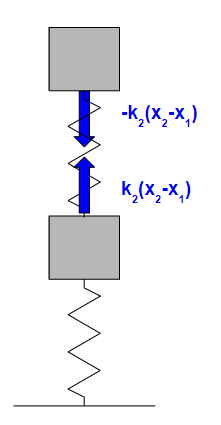
Be careful with the direction of the spring restoring forces.
When x2 moves further in the + direction than x1, spring k2 stretches and tries to restore, generating the reaction forces shown above.
We can rewrite them as:
$$ m_1\ddot{x_1}+(k_1+k_2)x_1-k_2x_2 = f $$
$$ m_2\ddot{x_2}+k_2(x_2-x_1) = 0 $$
Solving the Equations
As with the 1-DOF system, assume harmonic motion:
$$ x_1=X_1e^{iωt} $$
$$ x_2=X_2e^{iωt} $$
$$ f=Fe^{iωt} $$
Substitute these into the equations:
$$ -m_1ω^2X_1+(k_1+k_2)X_1-k_2X_2 = F $$
$$ -m_2ω^2X_2+k_2(X_2-X_1) = 0 $$
From the second equation, we find a relationship between
$$ X_1=(1-\frac{m_2}{k_2}ω^2)X_2 $$
Introduce the following parameters for simplicity:
$$ ω_1=\sqrt\frac{k_1}{m_1} $$
$$ ω_2=\sqrt\frac{k_2}{m_1} $$
$$ \frac{k_2}{k_1} = φ $$
After rearranging, we obtain:
$$ X_2=\frac{F}{k_1}\frac{1}{(1+φ-(\frac{ω}{ω_1})^2)(1-(\frac{ω}{ω_2})^2))-φ} $$
$$ X_1=\frac{F}{k_1}\frac{1-(\frac{ω}{ω_2})^2}{(1+φ-(\frac{ω}{ω_1})^2)(1-(\frac{ω}{ω_2})^2))-φ} $$
Interpretation
Parameter φ
ϕ\phiϕ represents the ratio between the two spring constants.
- When ϕ=0\phi = 0ϕ=0: The system reduces to the 1-DOF vibration model.
- When ϕ→∞\phi \to \inftyϕ→∞: k2→∞ \to \inftyk2→∞, leading to X1=X2.
- When k1→0 \to k1→0: Both masses move together in phase with the external force.
Even if we don’t design such extreme systems in real plants, checking whether your derived formula aligns with physical intuition is an essential engineering habit.
Natural Frequencies ω₁ and ω₂
These correspond to the natural frequencies of each subsystem when isolated.
Although this is a coupled system, using these parameters simplifies understanding and practical computation.
Meaning of X₁
When ω=ω2\omega = \omega_2ω=ω2, we find that X₁ = 0.
This means that although the external force acts on mass 1, it does not move — instead, mass 2 vibrates.
This is the fundamental concept behind vibration suppression (or damping).
In practice, X₁ never reaches zero, but minimizing it is the goal of vibration control design.
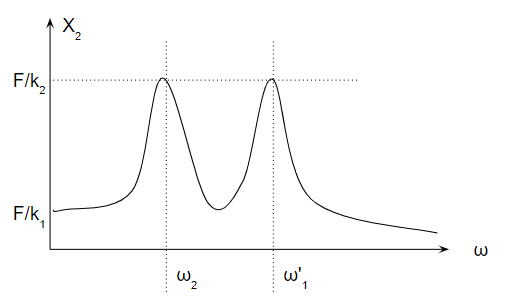
Frequency Response and X₂
The 2-DOF system has two resonance peaks, unlike the single peak of a 1-DOF system.
The number of peaks equals the system’s degrees of freedom — an important concept in vibration analysis.
When ω=0\omega = 0ω=0: X2=F/k1X_2 = F/k_1X2=F/k1.
When ω=ω2\omega = \omega_2ω=ω2: The first resonance (first mode).
When ω=ω1′=(k1+k2)/m1\omega = \omega’_1 = \sqrt{(k_1 + k_2)/m_1}ω=ω1′=(k1+k2)/m1: The second resonance (second mode).
In general, ω1′>ω1>ω2\omega’_1 > \omega_1 > \omega_2ω1′>ω1>ω2
Conclusion
In this article, we solved the equations of motion for a two-degree-of-freedom vibration system and discussed their physical meaning.
As variables increase, the math quickly becomes more complex.
However, by focusing on vibration control, we see that increasing degrees of freedom — and properly choosing mass and stiffness — allows us to design systems that effectively suppress unwanted motion.
In vibration engineering, more degrees of freedom mean more possible resonance modes — and more opportunities to optimize performance and stability.

Comments