“从储罐向外放流液体时,流量大概有多少?”
在现场进行放流作业、想要简单确认安全性时,这类问题偶尔会被提出。
乍一看似乎可以很快算出来,但实际上并不适合心算,仍然需要一定的计算过程。
本文将介绍一种适合现场手算、用于快速确认的计算思路。
真正遇到这种情况时,关键是保持冷静,按顺序思考。
本文属于管道流量计算系列以及流体力学系列的一部分。
计算对象模型
本次考虑的是在储罐底部连接软管并向外放流液体的系统。
使用软管通常是为了:
- 将放流液体集中到指定位置
- 避免液体流到通道或作业区域
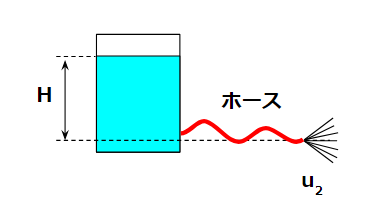
需要注意的是,与不使用软管直接放流相比,计算思路会有所不同。
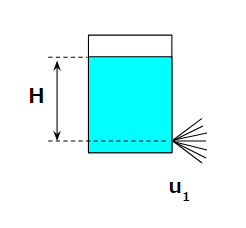
情况一:不使用软管放流
目标是求得流量,为此需要先计算流速。
在不考虑损失的情况下,可以利用能量守恒
$$ ρgH = \frac{1}{2}ρ{u_1}^2 $$
$$ u_1=\sqrt{2gH} $$
$$ Q_1 = \frac{π}{4}D^2u_1 $$
其中 D 为放出口(喷嘴)直径。
这就是不使用软管时的基本计算。
情况二:使用软管放流
如果连接了软管,就必须考虑软管内的压力损失。
虽然只多了一个项,但计算复杂度明显上升。
因此在现场,有时会直接套用“不带软管”的计算结果。
这种做法是否可行,需要根据具体情况判断。
数值计算示例
假设条件如下:
- 液位差:H = 1 m
- 管径:D = 0.05 m
不使用软管

这与经验法则一致:50A 管道、1 m/s 流速约为 100 L/min。
$$ ρgH = \frac{1}{2}ρ{u_2}^2 + 4f\frac{1}{2}ρ{u_2}^2\frac{L}{D} $$
$$ u_2=\frac{\sqrt{2gH}}{\sqrt{1+4f\frac{L}{D}}} $$
使用软管

$$ u_1=\sqrt{2*9.8*1}=4.5 m/s$$
$$ Q_1 = \frac{π}{4}*0.05^2*4.5*1000*60=521L/min $$
假设:
- 4f = 0.04
- 软管长度 L = 10 m
$$ 4f\frac{L}{D}=0.04*\frac{10}{0.05}=8 $$
$$ u_2=\frac{4.5}{\sqrt{1+8}} =1.5m/s$$
$$ Q_2 = \frac{π}{4}*0.05^2*1.5*1000*60=174L/min $$
仅仅加上一根软管,流量就会大幅下降。
即使软管较为光滑(例如 4f = 0.01),流速也只有约 2.6 m/s,
可以看出软管阻力对结果影响非常明显。
关于损失的理解方式
在本例中,正确评估压力损失是关键。
软管摩擦损失是最容易想到的,但在时间紧张时,连这一项都可能被忽略。
此外,还需要注意以下因素。
喷嘴处的急缩小损失
在不使用软管的计算中,通常忽略喷嘴处的急缩小损失。
简化计算假设流速不变,仅通过口径变化反映流量差异。
实际上,喷嘴越小,缩小损失越明显。
但由于涉及损失系数,这类计算在现场很少进行。
急扩大的损失
$$ \frac{1}{2}ρu^2 $$
$$ ρgH = \frac{1}{2}ρ{u}^2+\frac{1}{2}ρ{u}^2 $$
$$ u=\sqrt{gH} $$
考虑该损失后:
- 无软管:3.2 m/s,370 L/min
- 有软管:1.4 m/s,162 L/min
当存在明显的主损失(如软管摩擦)时,急扩大的影响相对较小。
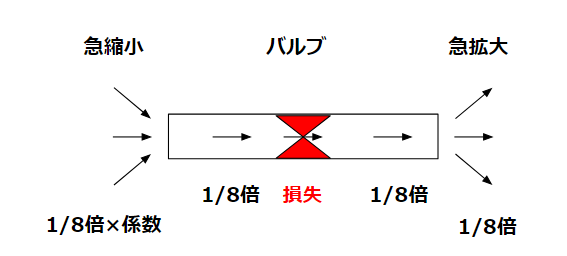
通过阀门节流
若在软管前后安装阀门并进行节流,则需要考虑阀门的压力损失。
严格计算应使用 Cv 值,但不适合现场手算。
现场可近似认为:流量=有效阀门面积×流速
这等同于改变喷嘴口径来考虑。
在这种情况下,阀门损失通常远大于软管及急缩小、急扩大的损失。
总结
本文介绍了使用软管从储罐放流液体时的流量计算思路。
要点如下:
- 以能量守恒为基础
- 软管摩擦损失对流量影响极大
- 急扩张、急缩小及阀门是否需要考虑,取决于具体工况
这是一个适合现场快速确认的手算方法,
对化工装置的设计、运行与维护都具有实用价值。

评论