計算フォームはこちらです。
流体流量と温度差から顕熱を計算する
比熱の公式は学生時代に習ったと思います。この式は、熱計算で非常によく使う基本式です。密度\(ρ\)、流量\(V\)、比熱\(c\)、温度差\(Δt\)を使って、顕熱\(Q\)は以下の通りに表せます。
$$ Q=ρVcΔt $$
熱交換器に流体を流して熱交換をしたとき、流体は温度変化を受けます。流量が少ないと温度変化量が高くなりますが、相変化が起きたり熱交換への影響が出たりと問題もあるので、一定の流量を確保しないといけません。配管口径を設計するためのに必要となる式です。
計算式は単純ですが、単位が合っているかどうかは常に確認しましょう。
$$ \frac{kcal}{h}=\frac{kg}{m^3}\frac{m^3}{h}\frac{kcal}{kgK}K $$
比熱を熱伝導率と勘違いしたり密度を計算に含めていなかったり、手計算だと間違えにくいけどもスプレッドシートや電卓で計算すると間違えがちです。
対数平均温度差を計算する
対数平均温度差は熱交換器の交換熱量計算に使います。
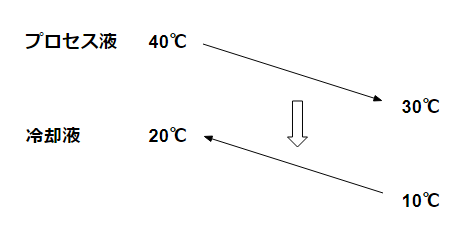
$$ Δt=\frac{(T_1-t_2)-(T_2-t_1)}{ln\frac{|T_1-t_2|}{|T_2-t_1|}} $$
多管式熱交換器など向流と並流では、計算式に違いがあります。現場的にはこの式をしっかり使うよりは単なる平均温度差で代用することの方が多いです。
$$ Δt=\frac{T_1+T_2}{2}-\frac{t_2+t_1}{2} $$
反応器のジャケットなど片側流体の温度が一定の場合も、無理して対数平均温度差にする必要はありません。
設備の熱計算は本来は微小区間に区切って微小伝熱量を計算し、微小区間ごとの温度変化を追っていって積分していけばいいのですが、大変です。これを代表温度で簡単に計算する時に、対数平均温度差を使うという位置づけです。
この場合でも流体の条件や汚れ係数などのファクターが入ってくるので、正確な計算はかなり大変です。
設備のキャパシティを決めるために、最大値を設計する際に使えなくは無いですが、それなら通常の算術平均でもそれなりの精度は出せそうです。
総括伝熱係数Uと伝熱面積Aと対数平均温度差Δtから交換熱量を求める
熱交換器の設計でほぼ不可欠な計算式です。
$$ Q=UAΔt $$
総括伝熱係数\(U\)と伝熱面積\(A\)と対数平均温度差\(Δt\)から交換熱量を求める式です。対数平均温度差\(Δt\)は1つ上の解説にもあるように、算術平均温度差を使う場合もあります。
総括伝熱係数\(U\)は境界層部+隔壁部+汚れ係数で計算されますが、計算式を現実に合わせるにはパラメータを適切に選ばないといけません。バッチ運転の場合、パラメータとなる温度や液量などは時々刻々変化するので、総括伝熱係数\(U\)も時々刻々変化するパラメータになります。
これを緻密に計算して、設計段階で運転条件を予測するということはあまり大きな意味はありません。エンジニアとしては、研究段階で開発された制御が十分できるだけの余裕を持った設備を設計することが大事で、総括伝熱係数\(U\)も仮定をおくことになります。
1.同様の運転条件で観測されたデータを\(U\)として使用して設計する
2.設備の最大能力として達成可能な\(U\)を計算する
このどちらかが設計指針となります。設備の設計としては2が大事で、運転をカバーできる設備であることを確認したら、付帯設備の設計のために1を使うというイメージです。
単位もしっかりチェックしておきましょう。
$$ \frac{kcal}{h}=\frac{kcal}{hm^2K}\frac{m^2}K $$
総括伝熱係数\(U\)は単位が複雑ですので、特に注意が必要です。Wの単位でも考えても構いませんが、化学物質の単位までWに統一して理解しておく必要があります。私は水の比熱を1で理解しているので、calの世界で考える方が都合が良いです。
冷凍機の消費電力と成績係数から冷凍能力を計算する
冷凍機の成績係数COPそのものです。計算はとても簡単です。
$$ COP=\frac{冷房能力}{冷凍機の消費電力} $$
冷凍機の能力はプラント建設時はしっかり決めていて、プロセスで使用する冷房能力と冷凍機で冷却できる能力(=プラントで処理できる最大の冷房能力)との大小関係を把握しています。ところが一定期間経って新製品が入ったり、既存製品を作らなくなったりすると、実際に必要な冷房能力とプラントで処理できる冷房能力の把握が難しくなります。
この場合でも、プラントの変動費合理化などを考える場合には、省エネとしての熱負荷の話題が出て扱いに困ることが多いです。そんな時にプロセスの熱負荷の解析をしたり、冷凍機の能力を調べようとすると、冷凍機の消費電力とCOPから概算を計算することがあります。
単純な計算式ですが、それでも十分に役経つ場面はあるでしょう。
反応器の液体を加熱・冷却するため必要な時間を計算する(温水・冷水)
機械の設計というよりはプロセスの設計の話です。とはいえ、機械の設計でもこの計算をしておくことはとても重要です。これまでと同じ構造の設備だからと熱計算の概念を忘れてしまうと、新しい検討をするときには困ってしまいます。
サイクルタイムの計算のために、簡単な熱計算をして問題ないことを確認するフォームです。
①プロセス側の加熱や冷却に必要な熱量を計算する
②伝熱能力を計算する
③ユーティリティの能力を計算する
この3つを満足して初めて問題ないと言えます。
①プロセス側の加熱や冷却に必要な熱量を計算する
$$ Q=ρVcΔt $$
の計算をしています。単位は\(kcal\)など熱量です。②と③は単位時間当たりの熱量ですので注意してください。反応器の容器内部の話です。容積\(V\)は液面を使っています。比熱\(c\)は溶媒の値を使い、水と油の混合物なら算術平均で良いと思いますが、大きい側の値で代用しても良いと思います。
②伝熱能力を計算する
$$ Q_{h1}=UAΔt $$
の計算をしています。単位は\(kcal/h\)など短時間当たりの熱量です。
総括伝熱係数\(U\)は熱交換器ハンドブックなどでは設備の形状を使った詳細計算をしていますが、ここではその結果もしくは概算値を直接入力することにしています。詳細計算は寸法の読み取りに時間が掛かる割に、その結果はこの式の\(U\)にだけ使うので、詳細に計算する必要があるかどうかしっかり考えましょう。
伝熱面積\(A\)は反応器内部の液体が容器と接触する面積を計算することになります。反応器内の容量と反応器の径から円筒胴として計算します。ジャケットの下鏡部も伝熱面積として算出しても良いかもしれませんが、計算が面倒ですので省略しても良いと思っています。省略した分だけ余裕として扱われます。
温度差\(Δt\)は算術平均を使っています。反応器内の温度は熱交換部で均一である(撹拌をしている)と仮定しているからです。ジャケット側は一定の温度差になると仮定します。この計算は、ジャケットで十分な用役が供給できると仮定したときに、熱交換できる最大量を計算するという意味になります。ジャケットの下鏡を計算しないことで、最大値を低い側に計算することになりますね。温水や冷水を使う場合、反応器の相変化を対象にはしていないので、反応器内部温度は温度変化の前後の平均値を使うと良いでしょう。反応気温度\(T\)、ジャケット温度\(t\)とすると
$$ T=\frac{T_1+T_2}{2} $$
$$ t= \frac{t_1+t_2}{2} $$
$$ Δt=|T-t| $$
①÷②の計算をすることで、サイクルタイムを計算します。②の温度部がそもそもプロセス全体の平均値であるので、サイクルタイムの計算も平均値となります。温度部を平均値で扱う以上、総括伝熱係数\(U\)を精密に扱う必要もないと思っています。
$$ h=\frac{Q}{Q_h} $$
③ユーティリティの能力を計算する
$$ Q_{h2}=ρV_hcΔt $$
の計算をしています。単位は\(kcal/h\)など短時間当たりの熱量です。①とは違ってジャケット側の計算です。②の計算でΔtを仮定していて、熱量Qも計算しているので、供給すべき流量\(V\)が計算できます。これだけの流量をジャケットに供給できない場合は、②の計算をやり直すことになります。通常はユーティリティの供給能力が大きいために、やり直し計算をすることにはならないはずです(なれば結構な問題です)。
反応器の液体を加熱・冷却するため必要な時間を計算する(スチーム)
スチームの場合は温水・冷水とは少し計算が違います。違う部分だけ解説します。
②伝熱能力を計算する
温度差\(Δt\)は温水・冷水だと温水・冷水の温度変化を考慮していましたが、スチームの場合は考慮しません。ジャケットがスチームで反応器内を加熱する場合、スチームは熱を奪われて凝縮します。ドレンとなった温水は熱交換に寄与はするものの、温水の温度が低下するというほどではありません(温水の熱量が反応器に伝わったとしても、ジャケット内部の水蒸気から温水に熱量が供給されるため)。
このため、温度差\(Δt\)は単純に以下で計算します。
$$ Δt = t – T $$
③ユーティリティの能力を計算する
ユーティリティの供給能力は温水・冷水の場合とは違って、スチームが不足する場合があります。十分に熱交換できる設備能力はあっても、供給するスチームを意図的に少なくしているという場合は、プロセスでは多々あります。
$$ Q_{h2}=ρV_hΔh $$
\(Δh\)は蒸発潜熱を示します。
設備としての伝熱可能な熱量とユーティリティの供給熱量の大小関係を比較して、サイクルタイムを計算するようにしています。ユーティリティ側が供給過剰な場合、実際に流れるユーティリティ流量は伝熱流量から以下のように決まります。
$$ Q_{h1}<Q_{h2} $$
$$ Q_{h1}=ρV_hΔh $$
放熱量を計算する
JIS A 9501 保温保冷工事施工標準の計算をしています。この計算は一度してしまうと、変更は簡単にはできないと思います。というのも、工場の設備や配管の施工時の保温厚みを決めてしまうからです。
詳細はこちらをご覧ください。保温材熱伝達率を直接入力する形にしています。材質によって微妙に変わりますが、私のプラントではほぼ同じ値です。
保温厚みを決める以外に、プラントの冷凍機能力の設定など熱量計算時に使う場合があります。とはいえ、冷凍機の冷凍能力の5%など仮定をおいてしまっても大きな問題は起きないでしょう。

コメント