在学习振动分析时,我们经常会接触到「时间响应」和「频率响应」两个概念。
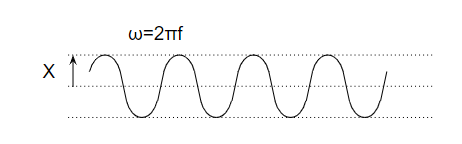
时间响应直观地表现出系统随时间的运动方式;
而频率响应则描述输入频率变化时,位移幅值如何变化。
很多工程师在学习过程中常常难以把这两者联系起来。
本文将帮助你建立时间响应与频率响应之间的联系,并理解共振与阻尼在实际设备中的作用。
正文
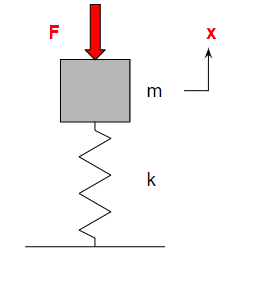
1. 一自由度振动系统的基本模型
我们先从最简单的**单自由度振动系统(SDOF)**开始。
它的运动方程为:
$$ m\ddot{x}+kx = 0 $$
$$ Fe^{iωt} $$
$$ X=X_0\frac{1}{1-(\frac{ω}{ω_0})^2} $$
这说明,位移与外力的频率 ω有关。
即使外力大小不变,频率不同也会导致振幅变化——这正是频率响应的核心思想。
2. 频率响应的物理意义
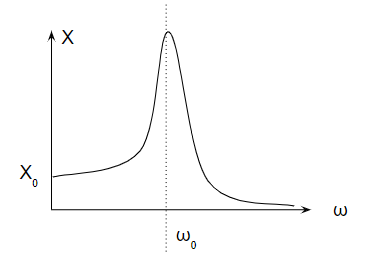
频率响应曲线显示了外力与位移之间的幅值比。
在低频下,位移较小;随着 ω 增加,振幅逐渐增大。
当 ω = ω₀(固有频率)时,理论上振幅趋于无穷大——这就是共振。
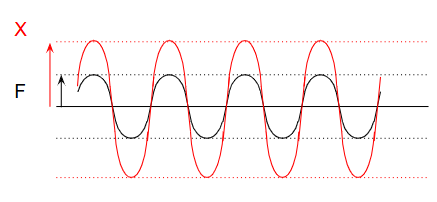
当然,实际中设备不会真正“无限振动”,而是在共振点附近可能出现结构损坏或异常。
当频率超过 ω₀ 后,振幅又会下降,这说明系统对不同频率的响应不同。
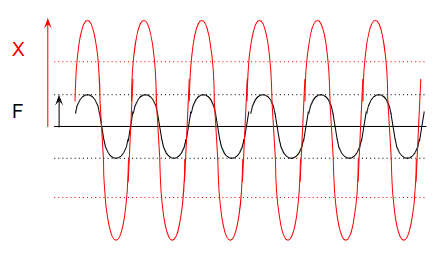
3. 考虑阻尼后的真实时间响应
在实际设备中,时间响应不会像理论图那样瞬间达到稳态。
通常,振幅会随着时间逐渐增加,最终趋于稳定。
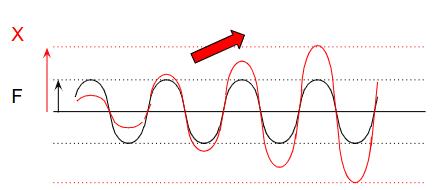
这是因为存在阻尼(粘性阻力),能量被不断耗散为热能或摩擦损失,
从而防止振动无限增长。
因此,加入阻尼后,理论与实际的响应曲线才真正吻合。
4. 如何避免共振——快速通过共振区
当 ω = ω₀ 时,系统容易产生危险的共振。
所以常听到一句话:
“要尽快通过共振转速区。”
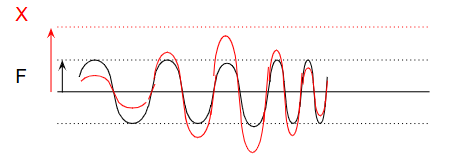
例如,小型电机启动后能迅速达到目标转速;
但大型旋转机械由于惯性大,加速过程较慢,
在共振频率附近停留时间较长,风险更高。
然而,共振并不会瞬间造成破坏。
如果系统快速加速越过共振区,振幅还未放大到危险值前就能脱离,
这样就能有效减少设备损伤。
总结
- 时间响应描述系统随时间的真实运动。
- 频率响应显示位移随激励频率变化的规律。
- 阻尼使振动稳定,防止振幅无限增长。
- 启动时快速通过共振频率,是避免损坏的关键。
理解时间响应与频率响应的关系,有助于我们在设计与实际操作中更准确地把握振动行为。

评论