在振动工程中，梁的运动方程是分析结构振动的基础。当梁上附加一个质量块或弹簧时，其振动特性会发生显著变化。
本文将系统介绍带质量块的梁的运动方程，通过数学模型与物理意义的结合，让你理解这种扩展模型的本质。
1. 基本运动方程
对于没有附加质量的梁，其运动方程为：
$$ ρA\frac{\partial^2 y(x,t) }{\partial t^2 }+EI\frac{\partial^4 y(x,t) }{\partial x^4 } = f(x,t) $$
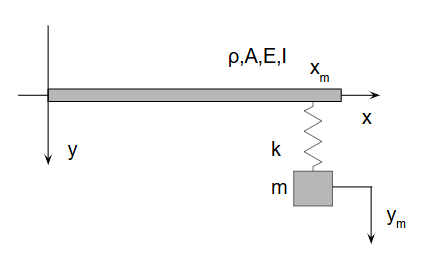
其中，ρ为密度，A为截面积，E为弹性模量，I为截面惯性矩。
若在梁的某一点 xm 处附加一个质量块 m，则系统需同时满足梁和质量块的运动方程：
$$ ρA\frac{\partial^2 y(x,t) }{\partial t^2 }+EI\frac{\partial^4 y(x,t) }{\partial x^4 } = k(y_m(t)-y(x_m,t)) $$
$$ m\frac{\partial^2 y_m(t) }{\partial t^2 } = -k(y_m(t)-y(x_m,t)) $$
这表示：梁在 xm 点受到来自弹簧的作用力，而质量块的位移 ym(t) 由该点的相对位移决定。
2. 方程的合并与变形
当我们将梁与质量块的方程相加时，弹簧力项相互抵消：
$$ ρA\frac{\partial^2 y(x,t) }{\partial t^2 }+EI\frac{\partial^4 y(x,t) }{\partial x^4 }+m\frac{\partial^2 y_m(t) }{\partial t^2 } = 0 $$
在数值计算中，y(x,t) 通常被离散化为有限节点的形式：
$$ \mathbf{y(x,t)}=\begin{pmatrix} y_{1}(t) \\ \dots \\ y_{n}(t) \end{pmatrix} $$
当增加一个质量块时，系统的自由度从 n 增加到 n+1：
$$ \mathbf{y'(x,t)}=\begin{pmatrix} y_{1}(t) \\ \dots \\ y_{n}(t) \\ \color{red}{y_{m}(t)} \end{pmatrix} $$
3. 特殊情况分析
(1) m = 0：无质量块
此时模型退化为普通梁的振动方程。检查该极限有助于验证方程合理性。
(2) m → ∞：刚性固定点
当质量无限大时，意味着该点无法运动，等价于固定边界。此时振动方程与两端固定梁一致。
质量块的位置 xm 不仅影响边界条件，也会改变系统的固有模态 ψ(x)。
当质量块接近梁端时，其影响更为显著，会导致固有频率下降，振型发生明显变化。
4. 模态与物理意义
在微分方程中，固有模态 ψ(x) 代表系统的自然振动形态。
附加质量块后，局部质量的增加改变了惯性分布，从而影响 ψ(x) 的形状。
这也是实际工程中在梁上安装设备或附加结构时必须考虑的关键点。
总结
带质量块梁的模型是单纯梁振动方程的自然扩展，能更真实地反映结构系统的动态特性。
- 通过引入质量块和弹簧，可以模拟设备附加质量或局部柔性支撑
- m=0 与 m=∞ 的极限情况帮助理解边界条件的物理意义
- 质量块的位置与大小会直接影响系统的固有频率与振型
理解这些基本原理，有助于在结构设计与动力分析中建立正确的理论模型。
评论