計算フォームはこちらです。
胴部の板厚計算(加圧側)
加圧側の胴部の強度計算は、タンクなどの容器の強度計算の基本です。
$$ t=\frac{PD_i}{2ση-1.2P} $$
圧力容器でも非圧力容器でも使用します。許容引張応力\(σ\)は一般に公開されている値を使用してください。単位は圧力と合わせる方が楽かもしれませんが、私が良く使っている単位で入力して計算式内で変換しています。
鏡部の板厚計算(加圧側)
加圧側の鏡部の強度計算は、圧力容器の計算でよく使用します。
$$ t=\frac{PDK}{2ση-0.2P} $$
胴部側より少し複雑な計算に見えますが、2:1半楕円だと\(K=1\)なので胴側の計算とほぼ同じ形に見えます。10%皿型だと\(h=0.194D\)なので、\(K=1.44\)となります。計算結果である必要板厚が少し下がる側になるので、2:1半楕円側で計算してアタリを付けても良いかもしれません。
撹拌軸の強度計算
撹拌軸の強度はしっかり計算しておかないと、運転中に折れるという問題が起きます。一般的な撹拌翼ならメーカーがしっかり計算してくれます。お手製の撹拌翼を作るときなどは、ユーザー側で計算する必要があるので、以下の式で計算しましょう。
$$ T=\frac{30W}{πN} $$
$$ M=\frac{1}{3}\frac{T}{d/2}a $$
$$ T_e=\sqrt{T^2+M^2} $$
$$ M_e=\frac{1}{2}(M+\sqrt{T^2+M^2}) $$
$$ σ_{max}=\frac{32M_e}{(1-n^4)πb^3} $$
$$ τ_{max}=\frac{16T_e}{(1-n^4)πb^3} $$
材料力学の教科書に掲載されている基礎的な式です。
アンカーボルト要否計算(地震)
アンカーボルトの要否計算をします。強度計算というと少し違うかも知れませんが・・・。
アンカーボルトは転倒計算とリンクします。タンクなどの重量が重たいものでも地震で傾いたときには、転倒する可能性があります。地震によって倒れようとする方向と自重によって元の位置に戻ろうとする力のバランスを考えます。
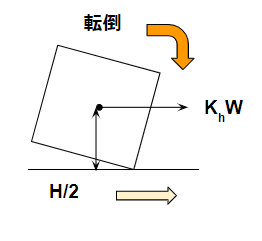 | 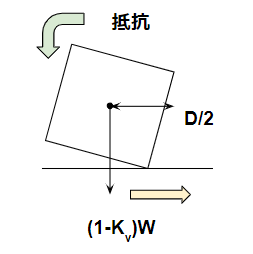 |
転倒側 $$ K_hW\frac{H}{2} $$
抵抗側 $$ (1-K_v)W\frac{D}{2} $$
設計水平震度\(K_h\)と設計鉛直震度\(K_v\)の2つの係数を使います。
判定条件は以下の式です。
$$ \frac{H}{D} < \frac{1-{K_h/2}}{K_h} $$
アンカーボルト要否計算(風)
地震ほどではありませんが風の力でも転倒する可能性があります。計算方法は自身と似ています。
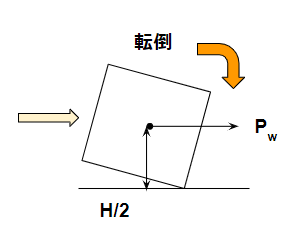 | 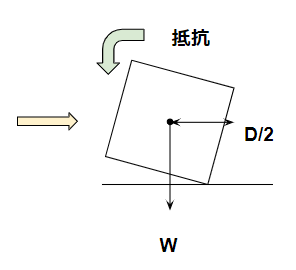 |
転倒側 $$ P_W\frac{H}{2} $$
抵抗側 $$ W\frac{D}{2} $$
風荷重\(P_W\)を計算するためには風力係数\(k\)が必要となります。
$$ P_W=k\sqrt{H}DH $$
\(DH\)は受圧面積を示します。
判定条件は以下の式です。
$$ P_W\frac{H}{2} < W\frac{D}{2}$$
配管の曲げ応力とたわみ計算
配管のサポート間隔を決めるために、材料力学の曲げ応力とたわみの式を計算します。
$$σ=\frac{M}{Z}=\frac{wl^2}{8Z}$$
$$δ=\frac{5wl^4}{384EI}$$
SGPなど汎用的なものなら、重量・寸法・ヤング率は表としてまとまっています。
評価としては以下が目安で良いと思います。
・たわみは2~3mmに抑える
・曲げ応力は10MPaを越えない

コメント