化学プラントや工業施設で配管を設置する際、サポートの強度と間隔を適切に設計することは、配管の安全性と耐久性に直結します。単に見た目や手の感覚で決めるのではなく、材料力学の基本原理を理解して計算することで、曲げ応力やたわみによるトラブルを未然に防ぐことができます。
本記事では、50A配管を例に、支持間隔を材料力学的に計算する方法を具体的に解説します。
手で触って簡単に揺れればサポートで固定という発想でも構いませんが、アタリを付ける意味でも支持間隔を知っておくことは助けになるでしょう。配管設計的にはハンドブックなどにある表を使う形になるでしょうが、計算例を紹介したいと思います。深く知りたい人向けですね。
具体的な計算はこちらのフォームをご利用ください。
この記事は、荷重シリーズの一部です。
タンク設計の基礎:風荷重と地震荷重の計算事例で学ぶ
機器荷重・ローディングデータの考え方|化学プラントの土木建築設計
架台強度計算の基礎と実務ポイント【初心者向け】
パイプスタンドの強度計算がこれで分かる!
パイプスタンドの強度計算と長期荷重・短期荷重
安易なラック継ぎ足しが招く落とし穴――強度・作業性・保守性の観点から考える配管設計の注意点
計算モデル
使用する計算モデルは以下の通りです。
- 50A
- SGP
- 内径52.9mm
- 常温
配管をサポートで支持する状況を想定しているので、機械力学の梁の両端支持の等分布荷重の式を使います。
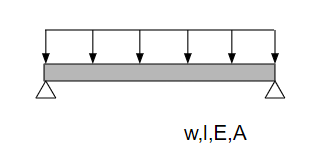
使用する計算式は以下の2つです。
曲げ応力
$$σ=\frac{M}{Z}=\frac{wl^2}{8Z}$$
たわみ
$$δ=\frac{5wl^4}{384EI}$$
この式は天から降ってきたものとして、ここでは取り扱います。計算上は断面二次モーメント\(I\)や断面係数\(Z\)の導出がカギとなります。
パラメータ
パラメータを1つずつ整理していきましょう。
縦弾性係数E
常温のSGP配管なので\(2×10^{11}N/m^2(200GPa)\)を使います。この数字も天から降ってきた数値です。温度によって多少振れがありますが、誤差範囲なので計算を簡単にするために丸めています。
重量\(w\)
重量\(w\)は単位長さ当たりの配管重量です。50AのSGP配管は内径52.9mm、厚み3.8mmですので、地道に計算しましょう。まずは断面積の計算をします。
π*(52.9/1000)*(3.8/1000)+π/4*(3.8/1000)2=(631+45)*10-6=677*10-6m2
鉄の比重が7850kg/m3なので、重量\(w\)は
677*10-6×7850=5.31kg/m
となります。
断面二次モーメント\(I\)
断面二次モーメントは中空円形断面の式を使います。
π/32*{(60.5/1000)4-(52.9/1000)4}=2.73×10-7m4(27.3cm4)
ここで50AのSGP外径は、52.9+3.8*2=60.5という数値を使っています。計算間違いや単位間違いをしたくないので、m単位で合わせるということを私は好んでいます。
断面係数\(Z\)
断面係数\(Z\)は、断面二次モーメントIを外半径で割ったものになります。
2.73×10-7/(60.5/2/1000)=9.03×10-6m3(9.03cm3)
曲げ応力\(σ\)
曲げ応力\(σ\)の計算をしましょう。先に\(l=1m\)の時の曲げ応力を最初に計算します。\(σ_0\)としておきましょう。\(l=1m\)なので、曲げ応力\(σ_0\)は
5.31/8/9.03×10-6×9.8=0.72×106Pa(0.72MPa)
となります。重力加速度\(9.8m/s^2\)を掛けている点に注意ですね。一般には曲げ応力が10MPaを越えないように支持間隔を決めます。
\(l\)を変化させればいいですが、\(σ_0\)の計算結果に\(l^2\)を掛ければいいだけです。ということで、
0.72×l2 < 10
という計算をすることになります。
l < √(10/0.72) = 3.72m
という計算結果から、曲げ応力の視点からは支持間隔は3.72m以下が要求されます。
たわみδ
たわみも同じように計算しましょう。l=1としたときのたわみをδ0とすると、
(5*5.31)/(384*2×1011*2.73×10-7)=26.55/20.9664=1.26×10-6m(1.23×10-3mm)
たわみは2~3mmに抑えることが求められます。
2 < 1.23×10-3*l4 < 3
という計算をします。
2/1.23×103 < l4 < 3/1.23×103 → 1.63×103 < l4 < 2.44×103 → 6.35 < l < 7.03
という結果になり、たわみの視点からは支持間隔は6.35m以下が要求される考えましょう。
まとめ
計算結果をまとめましょう。
- 曲げ応力 3.72m以下
- たわみ 6.35m以下
曲げ応力による制約の方が厳しく、50Aの場合3m~4m程度の間隔で支持するという思想になるでしょう。これと同じ計算をすれば、異なる口径でも求められます。計算自体は複雑ではありませんが、単位変換などミスが起こりかねませんね。
参考
関連記事
さらに知りたい方は、以下の記事をご覧ください。
最後に
配管サポートの設計では、材料力学に基づく曲げ応力とたわみの計算が非常に重要です。50A配管を例にした計算から、曲げ応力を考慮するとサポート間隔は3〜4mが目安となります。単に見た目で決めるのではなく、計算に基づいた設計を行うことで、長期的な安全性と保守性を確保できます。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。(コメント欄はこの記事の最下部です。)
*いただいたコメント全て拝見し、真剣に回答させていただきます。
この記事の内容を、あなたの職場・キャリアに合わせて整理したい方に技術・キャリア相談を行っています。海外プラント、製造管理、組織の病理、キャリア停滞など、あなたの状況に合わせて具体的にアドバイスします
→ 技術・キャリア相談はこちら
【著者:ねおにーーと】
化学プラントで20年以上、設計→製造→保全→企画まで一気通貫で経験したユーザー側エンジニア。 バッチプラントの設備・運転・トラブル対応を中心に、現場で本当に役立つ知識を発信しています。 → 詳しいプロフィールはこちら

コメント
配管のたわみ計算式の参照先はどの規格でしょうか。
コメントありがとうございます。
材料力学で一般に知られている式を使っています。
例えば以下のサイトなど、他にもさまざまなサイトでこの式を使っています。
https://kakunin-shinsei.com/deflection-formula/