パイプスタンドや柱の強度計算(strength calculation)に対する、基本的な考え方を解説します。
架台の強度計算と同じ発想で、材料力学の少し応用的な内容です。
材料力学を学んだ人向けですが、高校物理の力学の知識でも概要は理解できるでしょう。
オーナーエンジニアなら詳細計算をする機会は少ないので、細かい計算式は省略して、どういう考え方で計算するかを知っていれば十分でしょう。
地震荷重の考え方がやや特殊ですね。
パイプスタンド
化学プラントで使うパイプスタンドは、例えば以下のような形をしています。
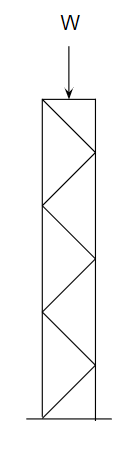
これがどういう計算をして決めているか考えていきましょう。
実際にはこの2本脚スタンド以外にも奥行き方向に延ばした4本脚スタンドにすることもあります。
逆に1本脚スタンドでは、単純な座屈の計算だけになります。
他にも門型スタンドなど派生形はいくつもあります。
なお、以下は今回の説明では省略します。
- 荷重はパイプと内容物の重量の合計(Wとする)
- 地震荷重はF(W×係数)
- 配管をまさに受けるサポート部分は、梁のたわみ計算で決める
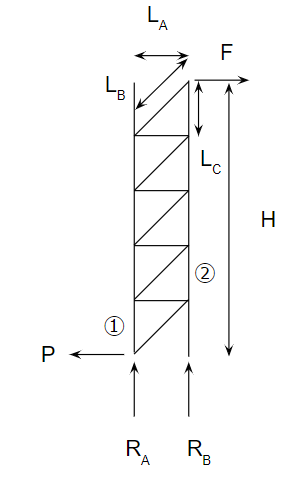
計算に使用する文字を紹介します。
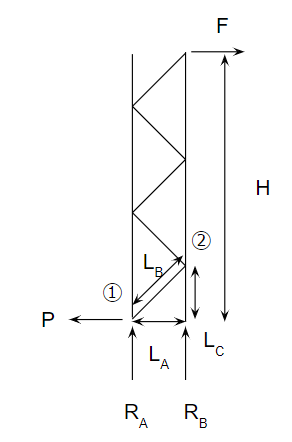
固定点の力
まずは固定点に発生する力である、RA・RB・Pを考えます。
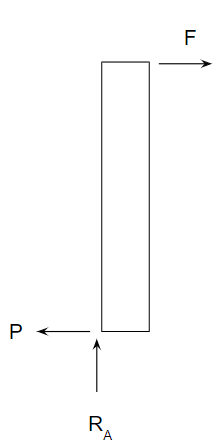
これは単純な物理の式そのものが使えます。
垂直荷重 \( R_A=-R_B=-FH/L_A \)
水平荷重 \( P=F \)
垂直荷重は力Fに対するモーメントを考えます。
水平荷重は力Fそのものです。
接点①
接点①(RAが作用する点)に掛かる力を見ていきましょう。
下の図の通りになります。
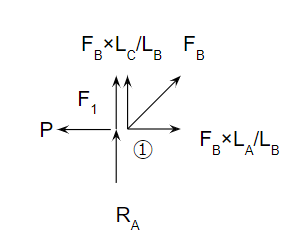
RAとPは上で述べたそのもの。
接点①では垂直部材からの力F1と斜材からの力FBをそれぞれ受けます。
これらの力の釣り合いを考えます。
長さについては斜辺LB・水平LA・垂直LCという三角形を考えると分かりやすいでしょう。
F1+FB×LC/LB+RA=0
P-FB×LA/LB=0
下の式から
$$ F_B=P\frac{L_B}{L_A}=F\frac{L_B}{L_A} $$
となり、上の式から
$$ F_1= -F_B\frac{L_C}{L_B}-R_A=-F\frac{L_C}{L_A}+F\frac{H}{L_A}=F\frac{H-L_C}{L_A} $$
となります。
接点①で斜材からの力の分だけ、垂直部材が受ける垂直荷重は小さくなります。
斜材も垂直部材も地震荷重Fよりも大きな荷重が作用します。
斜材の角度を緩やかにするほど、斜材に掛かる力は弱くなりますが、垂直部材で緩和される力は小さくなります。斜材の数を増やして、斜材を細くするというイメージです。
接点②
接点②も同じように考えましょう。
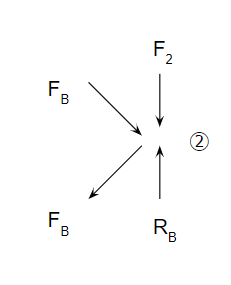
接点②では2つの斜材部が結合されます。
水平方向の釣り合いを取るためには、下の斜材部が図の左方向に作用している以上、上の斜材部は図の右方向に作用することとなります。
言い換えると、下の斜材は圧縮されるのに対して上の部材は引張を受けます。
斜材の取付角度が同じなら、上の斜材も下の斜材も同じ力FBとなります。
垂直荷重F2を計算しましょう。
$$ F_2+2F_B\frac{L_C}{L_B}=R_B $$
$$ F_2=R_B-2F_B\frac{L_C}{L_B}=F\frac{H}{L_A}-2F\frac{L_C}{L_A}=F\frac{H-2L_C}{L_A} $$
斜材がサポートしてくれる形で、垂直荷重が少なくなっているのが分かるでしょう。
以降の計算は繰り返しとなります。
接点番号をnとすると、以下の関係になります。
$$ F_n=F\frac{H-nL_C}{L_A} $$
垂直応力の評価
一般にはスタンドは同じ断面積・断面二次モーメントの一つの構造物で作るので、計算では最も下の垂直荷重が高い部分で(RA)で考えると良いでしょう。
$$ σ=\frac{R_A}{A}= \frac{F}{A}\frac{H}{L_A} $$
既存のパイプスタンドのちょっと足したいというケースは、増改築で非常に多いです。
こういう場合に備えて、パイプスタンドは大きめに余裕を持っておきましょう。
特殊なパイプスタンド
稀な例ですが、以下のようなパイプスタンドを見かけます。
文字は変えずに形だけ変えて計算してみましょう。
$$ P=F $$
$$ R_A=-R_B=-F\frac{H}{L_A}$$
$$ F_B=F\frac{L_B}{L_A} $$
$$ F_1=F\frac{H-L_C}{L_A} $$
これらは変わりません。
次の接点②が変わります。
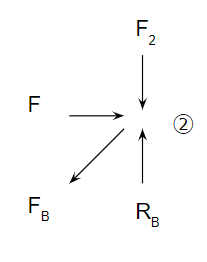
水平方向は
$$ F_B\frac{L_A}{L_B}=F $$
となります。この力は引張の方向です。
以下も同じように進めると、斜材側は常にFBの圧縮を受け、水平の補強材は常にFの引張を受けることになります。
$$ F_2+F_B\frac{L_C}{L_B}=R_B $$
$$ F_2=F\frac{H-L_C}{L_A} $$
斜材の数が少ない分だけ、接点での垂直応力は高くなります。
それでも最大の垂直応力自体はRAで変わりありませんので、柱の部材そのものは変わりません。
こんな感じの考え方をします。
実際にはもう少し複雑な条件になっていて、簡単にするために安全側の省略をしている部分があります。
参考
関連記事
最後に
パイプスタンドや柱の強度計算の基本的な考え方を解説しました。
トラスの考え方で力とモーメントの釣り合いを考えます。
斜材による力の伝わり方が変わる部分と変わらない部分があるのが興味深いです。
詳細の計算をしないエンジニアでも力学の応用として概要は知っていても良いと思います。
化学プラントの設計・保全・運転などの悩みや疑問・質問などご自由にコメント欄に投稿してください。（コメント欄はこの記事の最下部です。） *いただいたコメント全て拝見し、真剣に回答させていただきます。