When studying vibration analysis, we often discuss time response and frequency response.
Time response feels intuitive because it shows how things actually move over time,
while frequency response focuses on how displacement changes with input frequency.
However, many engineers find it hard to connect these two views.
This article bridges that gap — helping you visualize how a system’s vibration behavior in time directly relates to its frequency response and resonance.
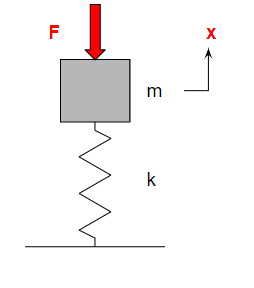
1. The Basic One-Degree-of-Freedom Model
Let’s start with the simplest vibration system: a single degree of freedom (SDOF) model.
Its motion equation is:
$$ m\ddot{x}+kx = 0 $$
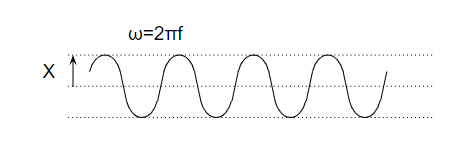
$$ Fe^{iωt} $$
$$ X=X_0\frac{1}{1-(\frac{ω}{ω_0})^2} $$
This shows that displacement depends on the excitation frequency ωωω.
Even if the force magnitude stays constant, the vibration amplitude changes with frequency — this is the essence of the frequency response.
2. What Frequency Response Really Means
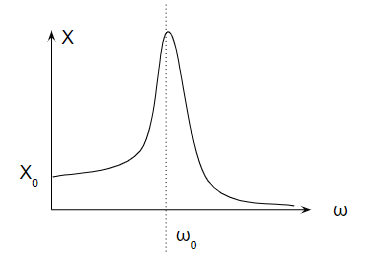
A frequency response plot shows the amplitude ratio between the force and the resulting displacement.
At low frequencies, displacement is small.
As ωωω increases, the amplitude rises — reaching infinity (theoretically) at ω=ω0, known as the resonance frequency.
In practice, the system doesn’t actually go to infinity — the spring or structure would fail first.
Once the excitation frequency exceeds ω0ω_0ω0, the displacement decreases again.
This curve describes how the system “filters” vibration depending on frequency.
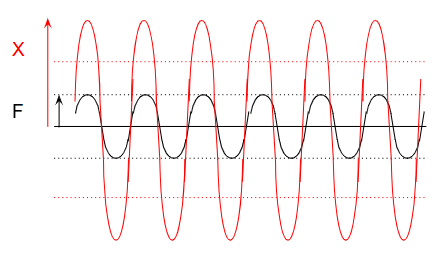
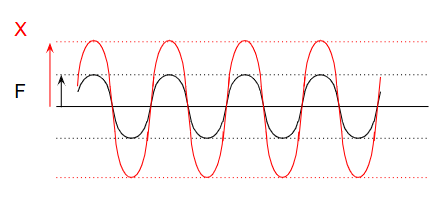
3. The Real Time Response (Including Damping)
In real-world machines, the time response doesn’t instantly show the steady-state oscillation seen in textbooks.
Instead, the vibration amplitude gradually grows and eventually stabilizes.
This happens because of viscous damping —
energy is continuously dissipated as heat or friction, preventing infinite vibration buildup.
The damping effect connects the clean mathematical model to the behavior we actually observe in machinery.
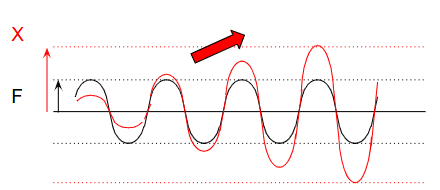
4. Avoiding Resonance — The Role of Acceleration
At resonance ( ω=ω0), vibration amplitudes can grow dangerously high.
That’s why it’s often said:
“Pass through the resonance speed as quickly as possible.”
For example, small motors reach their target speed almost instantly.
But large rotating equipment takes longer to accelerate due to inertia.
During this slow acceleration, the machine may spend time near its resonant frequency — a risky situation.
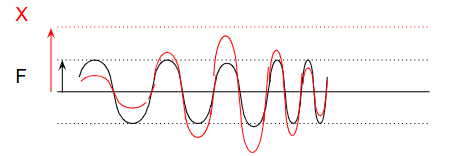
However, resonance doesn’t cause failure immediately.
If the system quickly accelerates beyond the resonant frequency, displacement doesn’t have time to grow large.
Thus, fast acceleration helps avoid excessive vibration during startup.
Conclusion
- Time response shows how a system moves in real time.
- Frequency response shows how amplitude changes with excitation frequency.
- Damping stabilizes vibration and prevents runaway amplitude.
- Rapid acceleration through the resonant frequency minimizes vibration damage.
By understanding how these concepts connect, engineers can visualize both simulation and real motion — improving both design and operation of vibrating systems.

Comments