計算フォームはこちらです。
流速から配管圧力損失を計算します
配管摩擦損失の基本式ともいえる以下の式を計算するものです。
$$ ΔP=4f\frac{1}{2}ρv^2\frac{L}{D} $$
圧力損失の単位によって表現が多少異なりますが、エネルギー単位のこの表現が私は一番分かりやすいと思っています。物理の位置エネルギーや運動エネルギーからの単純な派生形として見やすいからですね。
配管摩擦係数\(4f\)は近似式も作れますが、moody線図から読み取った値を入力するフォームにしています。\(Re\)がある程度以上高いと、ほぼ定数として扱えるのでグラフを読む機会は私はそう多くはありません。
流速\(v\)を標準流速に抑えている限り、配管長さ\(L\)と配管口径\(D\)で決まる値になって、密度\(ρ\)が高くない限りは、大きな値になることはほぼないということが感覚的に分かればこの計算を真面目にする必要性が低くなっていくでしょう。
液高さから自然流下する場合の流量を計算します
自然流下の計算は圧損計算が含まれる点で少し注意が必要です。
$$ h_2-h_1=4f\frac{1}{2}ρv^2\frac{L}{D} $$
液高さは反応器内の液を含めない方が無難です。下の図で言う1回目の左の容器に着目すると容器内の液高さを含めて計算したくなってきますが、2回目の左の容器のように容器内に液が入っていない条件を考える方が良いです。
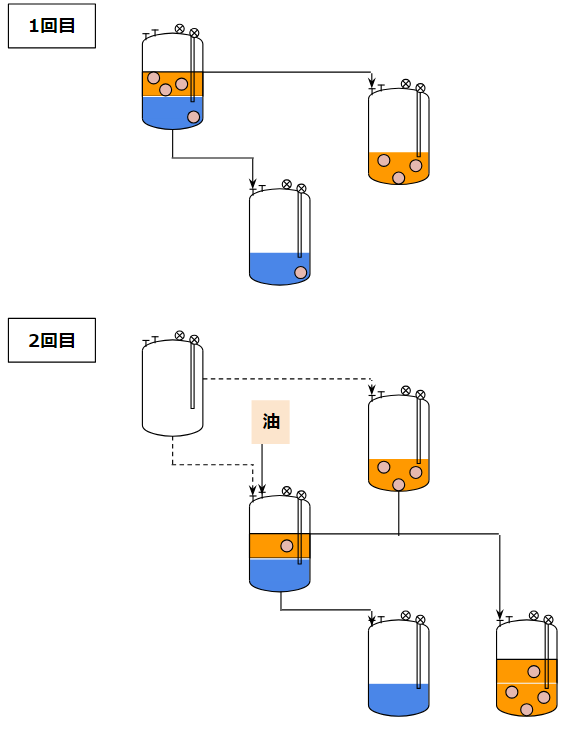
これは前提として自然流下のラインには調整弁があって、流速制限を掛けるからです。容器内の液高さを含めると流速が上がる結果になりますが調整弁を絞ることで目的の流速に抑え、液高さが少なくなってきた時には調整弁を開いて流速を確保しようとします。このため、条件が悪い側でも運転が可能なように配管口径を決めておくアプローチが求められます。
自然流下の計算は
・液高さが駆動源 \(h_2-h_1\)
・流量が運転条件から与えられる
・口径を仮定
・流速を計算(圧力損失)
・流速が範囲内に入っていることを確認
というアプローチをします。流速が高すぎるとガス巻き込みをして運転に支障が出てしまいます。
一方でポンプの計算は
・ポンプが駆動源
・流量が運転条件から与えられる
・口径を仮定
・流速を計算(圧力損失)
・揚程を計算
というアプローチが一般的で、揚程がかなりの範囲で選ぶことができます。ポンプの計算を見ていると口径の設計は2次的な要素に見えますが、実際には1次的な要素であると思っています。プラント設計とか設備の統一性という点から見ると、むしろ揚程が2次的な要素という印象。
抵抗係数(相当長)を計算します
配管摩擦損失の計算は、①直管と②その他の合計で計算されます。②その他は、エルボ・チーズなどのフィッティングやバルブなどの直管以外の配管部品です。これらの部品も摩擦損失を持ちますが、個々に計算式を設定するのは大変なので「直管の何mに相当するか」という相当長に置き換えます。
$$ ΔP=K_a\frac{1}{2}ρv^2 $$
抵抗係数\(K_a\)は部品の種類だけでなく口径でも違うという捉え方がありますが、口径はおよそ平均的な値で近似して部品の種類ごとに1つの値にしたものが簡便です。この考え方は、抵抗係数は精度を高く摩擦損失を求めるものではなく、本来の摩擦損失の計算自体がかなりの余裕を含めて設計しなければいけないことを示しています。
$$ ΔP=4f\frac{1}{2}ρv^2\frac{L}{D}+K_a\frac{1}{2}ρv^2 $$
直管の摩擦損失の\(4f\)をmoody線図を使って緻密に求めても、効果はあまり高くありません。バルブやフィッティングの数を緻密に数えるのも、時間が掛かって問題です。この計算をしている段階は設備設計であって、その後の配管設計で具体的な数が決まってくるから、ある程度多めに個数を設定することになるでしょう。
ポンプのNPSHaveを計算します
ポンプのNPSHaveの計算も、何か特別なことをしているように見えますが、分解すると圧力損失の計算と同じことに気が付くでしょう。
$$ NPSH_{ave} > NPSH_{req} $$
であることを担保する計算です。\(NPSH_{req}\)がポンプ内で発生する圧力損失で、\(NPSH_{ave}\)が配管ライン側で持っている余裕。\(NPSH_{ave}\)が少ないとポンプ内で真空状態になってキャビテーションが起きるために、ポンプ運転に問題が起きる可能性があります。\(NPSH_{ave}\)の計算は、ポンプ直前の液体の圧力と液体の蒸気圧の大小を比較しています。
$$ ポンプ直前の液体圧力 > 液体の蒸気圧 $$
であればいいという計算をします。ポンプ直前の液体圧力は
$$ ポンプ直前の液体圧力 = タンク内の液体圧力 – ΔP $$
という関係になるので、\(ΔP\)である圧力損失を計算しようということになります。
$$ ρgh_1+P_1=ρgh_2+P_2+4f\frac{1}{2}ρv^2\frac{L}{D}+ρgNPSH_{ave} $$
であって、\(h_2=0\)、\(P_1=101.3kPa\)とすると、
$$ NPSH_{ave}=h_1+\frac{101.3}{ρg}-\frac{P_2}{ρg}-4f\frac{1}{2}\frac{v^2}{g}\frac{L}{D} $$
となります。\(h_1\)は自然流下と同じで容器内の液高さを含めない方が安全側です。\(P_2\)が高い(温度が高い)場合には、\(ΔP\)がいくら少なくても\(NPSH_{ave}\)が小さいので、危険と考えられます。少しでも余裕を持たせるために\(ΔP\)を下げる狙いで配管口径を上げたり、容器そのものの高さを上げたりと工夫をするかどうかの判定に使うのが、\(NPSH_{ave}\)の計算でしょう。

コメント