計算フォーム「流量計算」の解説

計算フォームはこちらです。

送液量と送液時間から送液に必要な流量を計算します

　タンクに入っている液体を別のタンクにポンプで輸送する場合を考えています。

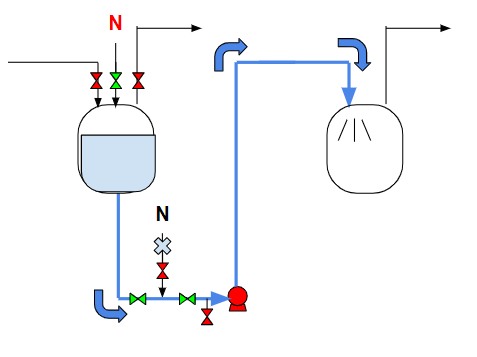
　タンクの液量を\(V\)、ポンプの流量を\(Q\)としたとき、送液時間\(t\)は

$$ t=\frac{V}{Q} $$

で計算できます。
　サイクルタイムの計算上は、ポンプの起動停止の時間や予備の時間も含めますが、最初に送液時間の計算をしてから考えます。
　送液に掛かる時間が長いなら、ポンプの能力を上げたり配管口径を上げたりという次のチェックに入ります。

配管口径と平均流速から体積流量を計算します（スチーム以外）

　配管口径と平均流速から単純に流量を計算する場合を考えます。

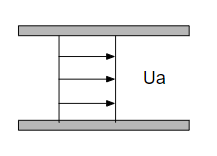
　配管口径\(d\)、平均流速\(u\)としたときに体積流量\(V\)は

$$ V=\frac{π}{4}d^2u $$

で計算できます。平均流速\(u\)はおおよそ以下の値です。

　水など粘度が小さいもの：1～2m/s
　硫酸など粘度が高いもの：0.5～1m/s

配管口径と平均流速から質量流量を計算します（スチーム）

　スチームの場合も上記と考え方は同じです。ただし、スチームの場合はm3/hなどの体積流量ではなくkg/hなどの質量流量で議論されるため、密度を掛けてあげる必要があります。
　密度を\(ρ\)とすると、質量流量\(V\)は

$$ V=ρ\frac{π}{4}d^2u $$

で計算できます。平均流速\(u\)は10～30m/sの範囲が一般的です。

　大抵の場合は飽和蒸気で扱うので、スチームの蒸気圧が分かれば飽和水蒸気圧（飽和温度）から蒸気表を使って、密度を算出できます。蒸気表は検索で容易にヒットします。

集気ラインの流量を計算します

　集気ラインや集塵ラインなど減圧された配管の末端部を、掃除機のように使うケースは現場では多いです。

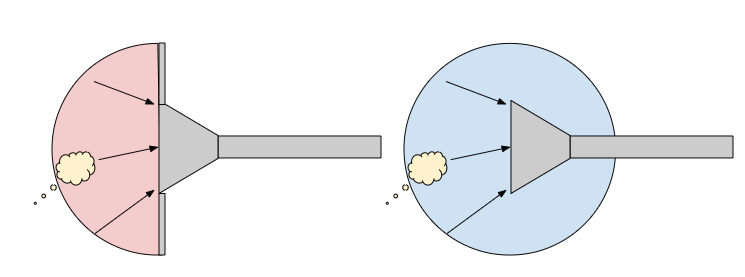
設計は以下の2段階で行います。

1. 吸引能力の設計
2. 配管口径の設計

1.吸引能力の設計

末端部の口径\(d_1\)に対して、吸引流量\(V_1\)は以下で計算します。

$$ V_1=\frac{π}{4}d_1^2u_1 + \frac{1}{2}2πd_1\frac{π}{4}u_1^2$$

\(u_1\)は制御風速で0.5～1.0m/sが一般的です。以下の考え方の近似計算です。

中央部は直径\(d_1\)で高さ\(u_1\)の円柱、周囲部は半径\(u_1\)の半円を直径\(d_1\)で積分した半ドーナツ形状で考えます。

2.配管口径の設計

1で必要な吸引能力を決めた後、配管口径\(d_2\)の設計をします。風速が10m/sになるように口径を決めます。

$$ V_1=\frac{π}{4}d_2^210 $$

口径が大きいと圧力損失が下がりますが、線速が落ちるので吸引できなくなります。必要な線速を確保するためには、真空源の能力が適正である必要があることに注意しましょう。

熱交換器のチューブ本数とバッフル間隔を計算します

　熱交換器の設計として、①伝熱面積を求める計算と②伝熱面積から熱交換器の寸法を求める計算の2つに大きく分かれます。この②の計算をします。

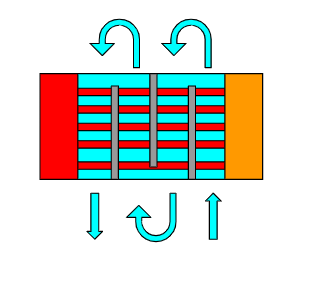
チューブ本数の計算

　伝熱面積\(A\)を決めたら、チューブ長さ\(L\)とチューブ口径\(d\)とチューブ本数\(N\)を決めます。チューブ長さ\(L\)はチューブ口径\(d\)から強度計算により決定するのが本来ですが、現実的なチューブ長さとチューブ口径を仮定してしまいます。

　私が良く扱う10～30m²クラスの熱交換器だと、チューブ長さ\(L\)は2～3mくらい、チューブ口径\(d\)は25Aくらいです。ここまで決まるとチューブ本数\(N\)が計算できます。

$$ N=\frac{A}{πdL} $$

　チューブ内の流速をチェックして1.0m/s以下であればとりあえずOK、1.0m/s以上であればチューブ長さ\(L\)とチューブ口径\(d\)を調整するという簡易的な設計方法です。

シェル径の計算

　シェル側の流量を計算するために、チューブ本数\(N\)からシェル径\(D\)を先に求めます。四角配列で簡略化します。

　管板の1/4のエリアにチューブ本数の1/4が割り当てられるので、この領域を考えます。この1/4円の半径部に相当する管板の水平軸もしくは垂直軸に配列されるチューブ\(N_1\)としましょう。1/4円に並ぶチューブ本数は、

$$ \frac{N_1(N_1+1)}{2} $$

で計算できます。1/4円でこの本数なので円全体（管板全体）を考えると、以下の式が成立します。

$$ N=2N_1(N_1+1) $$

ここから\(N_1\)が求まるので、シェル径を求めます。これも簡易的に以下の式を使います。

$$ D=(d+0.004)N_1+0.05*2 $$

　0.004という定数はチューブ間の隙間で4mmであることを示し、0.05という定数は外周部チューブとシェルの間の隙間で50mmであることを示します。この辺は概算値です。

バッフル間隔の計算

　シェル径\(D\)が決まったらバッフル間隔\(B\)を決めます。バッフル間隔\(B\)とシェルに流れる流量\(Q\)を与えて、シェルのバッフル間を流れる流速\(v\)を計算します。

$$ v=\frac{Q}{B(0.004N_1+0.05*2)} $$

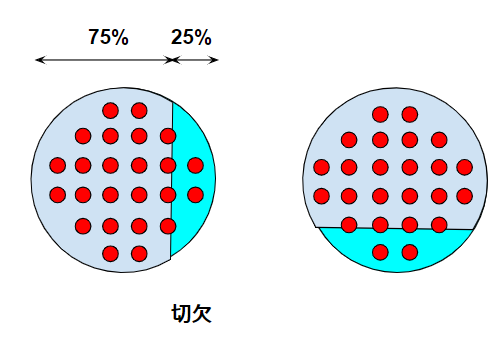
　断面方向は4mmのチューブ間隙間と50mmのシェル部との隙間、長手方向はバッフルで仕切られた区域を、シェル流体が流れるます。シェルが流れる領域の最大断面積を計算して、流速を計算していることになります。流速判定は最小断面積（最大流速）で判定する方が良いと思いますが、今回は採用していません。バッフルは例えば25%切り欠き円などですので、最小断面積は最大断面積の\(\sqrt{3}/2\)くらいになるはずです。